Αυτοόμοια Σύνολα

Μιλώντας μη αυστηρά, ένα υποσύνολο του $\mathbb{R}^n$ είναι αυτοόμοιο αν μπορεί να χωριστεί σε κομμάτια που είναι όμοια με το ολόκληρο (αρχικό) σύνολo. Τα σύνολα Cantor είναι ένα απλό παράδειγμα. Αν τα ((κομμάτια)) $C(\lambda )\cap [0,\lambda ]$ και $C(\lambda )\cap [1-\lambda,1]$ τα μεγενθύνουμε κατά $1/\lambda$ θα πάρουμε το αρχικό σύνολο Cantor.

Η αυτοoμοιότητα του $C(\lambda)$ μπορεί να γραφεί μαθηματκά με τον τύπο

$$C(\lambda)=f_1[C(\lambda)]\cup f_2[C(\lambda)]$$

όπου οι συναρτήσεις ομοιότητας $f_1,f_2:\mathbb{R}\rightarrow \mathbb{R}$ είναι $f_1(x)=\lambda x$ και $f_2(x)=\lambda x +1-\lambda$.

Απόδειξη: Αν συμβολίσουμε με $C_k(\lambda)$ το σύνολο στο $k$-οστό βήμα, δηλαδή $C_k(\lambda)= \cap_{i=0}^{k}\cup_{j=1}^{2^i}I_{i,j}$, τότε από επαγωγή έχουμε ότι $C_{k+1}(\lambda)=f_1[C_k(\lambda)]\cup f_2[C_k(\lambda)]$ για $k=0,1,\ldots$.

Πρώτα θα δείξουε ότι $C(\lambda )\subseteq f_1[C(\lambda)]\cup f_2[C(\lambda)]$. Έστω $x\in C(\lambda )$. Τότε $x\in C_1(\lambda )$. Άρα είτε $x\in [0,1/3]$ είτε $x\in [2/3,1]$. Θεωρούμε την δεύτερη περιπτώση, όπου δηλαδή $x\in [2/3,1]$, η άλλη περίπτωση είναι παρόμοια. Τώρα για οποιοδήποτε $k$, ξέρουμε $x\in C_{k+1}(\lambda )=f_1[C_k(\lambda)]\cup f_2[C_k(\lambda)]$. Όμως $f_1[C_k(\lambda)]\subseteq f_1[[0,1]]=[0,1/3]$, έτσι στην πραγματικότητα $x\in f_2[C_k(\lambda )]$ ή $(1/\lambda)x -1/\lambda +1 \in C_k(\lambda )$. Αυτό ισχύει για όλα τα $k$, άρα $(1/\lambda)x-/\lambda +1 \in \cap_{k\in\mathbb{N}}C_k(\lambda )=C(\lambda )$. Έτσι $x\in f_2[C(\lambda )]$. Άρα έχουμε ότι $x\in f_1[C(\lambda)]\cup f_2[C(\lambda)]$.

Στη συνέχεια θα δείξουμε ότι $C(\lambda )\supseteq f_1[C(\lambda)]\cup f_2[C(\lambda)]$. Έστω $x\in f_1[C(\lambda)]\cup f_2[C(\lambda)]$. Τότε είτε $x\in f_1[C(\lambda )]$ είτε $x\in f_2[C(\lambda )]$. Παίρνουμε τη δεύτερη περίπτωση. Έτσι $(1/\lambda)x-/\lambda +1 \in C(\lambda )$. Τώρα για οποιοδήποτε $k$, ξέρουμε $(1/\lambda)x -1/\lambda +1 \in C_k(\lambda )$ ή $x \in f_2[C(\lambda )]\subseteq C_{κ+1}(\lambda )$. Έτσι $x\in \cap_{k\in\mathbb{N}} C_{k+1}(\lambda )=\cap_{k\in\mathbb{N}}C_k(\lambda )=C(\lambda )$. Αυτό ολοκληρώνει την απόδειξη ότι $C(\lambda ) = f_1[C(\lambda)]\cup f_2[C(\lambda)]$. $\Box$

Θα δώσουμε τώρα πιο αυστηρούς ορισμούς.

Ορισμός 3.4.1   Λίστα λόγου είναι μια πεπερασμένη ακολουθία θετικών αριθμών $(r_1,r_2,...,r_n)$. Την λίστα λόγου θα τη λέμε συστελλόμενη ή υπερβολική αν και μόνο αν $r_i<1$ για όλα τα $i=\{1,...,n\}$.

Ορισμός 3.4.2   Σύστημα Επαναλαμβανόμενων Συναρτήσεων (I.F.S. = iterated function system), εφαρμοσμένων πάνω σε μια λίστα λόγου $(r_1,r_2,...,r_n)$ στο μετρικό χώρο $(X,\rho)$, είναι μια ακολουθία συναρτήσεων $(f_1,f_2,...,f_n)$, όπου $f_i:X\rightarrow X$ είναι ομοιότητα με λόγο $r_i$, δηλαδή ισχύει $\rho(f_i(x),f_i(y))=r_i\rho(x,y)$ για $x,y\in X$ και $i\in\{1,...,n\}$.

Ορισμός 3.4.3   Ένα μη κενό συμπαγές υποσύνολο $K$ του $X$ είναι αναλλoίωτο σύνολο για το σύστημα επαναλαμβανόμενων συναρτήσεων $(f_1,f_2,...,f_n)$ στο μετρικό χώρο $X$ αν και μόνο αν

$$K=\bigcup_{i=1}^{n}f_i[K]$$

Κάθε τέτοιο αναλλοίωτο σύνολο είναι αυτοόμοιο.

Θα δείξουμε ότι κάθε σύστημα επαναλαμβανόμενων συναρτήσεων εφαρμοσμένο σε μια συστελλόμενη λίστα λόγου, ορίζει μοναδικό (μη κενό) συμπαγές αναλλοίωτο σύνολο. Αυτό σημαίνει, για παράδειγμα, ότι το σύνολο Cantor $C(1/3)$ ορίζεται ακριβώς ως συμπαγής αναλλοίωτο σύνολο για το σύστημα επαναλαμβανόμενων συναρτήσεων $\{f_1(x)=(1/3) x, f_2(x)=(1/3)x+2/3\}$.

Θεώρημα 3.4.1   Έστω $X$ πλήρης μετρικός χώρος και έστω $(f_1,f_2,...,f_n)$ ένα σύστημα επαναλαμβανόμενων συναρτήσεων στο $X$ εφαρμοσμένο σε μια συστελλόμενη λίστα λόγου $(r_1,r_2,...,r_n)$. Τότε υπάρχει μοναδικό μη κενό συμπαγές αναλλοίωτο σύνολο $Κ$ για το σύστημα επαναλαμβανόμενων συναρτήσεων στο μετρικό χώρο $(\mathcal{K}(X),D)$, των μη κενών συμπαγών υποσυνόλων του $X$, με μετρική Hausdorff (βλέπε θεώρημα 1.9.1).

Μάλιστα αν ορίσουμε μια ακολουθία συνόλων $A_k$ ως εξής: $A_0$ είναι μη κενό συμπαγές υποσύνολο του $X$, $A_1=\cup_{i=1}^{n}f_i[A_0]$ με αναδρομικό τύπο $A_{k+1}=\cup_{i=1}^{n}f_i[A_k]$, τότε

$$K=\lim_{k\rightarrow \infty}A_k$$

όπου το όριο λαμβάνεται βάσει της μετρικής Hausdorff.

Απόδειξη: Θεωρούμε το μετρικό χώρο $\mathcal{K}(X)$ των μη κενών συμπαγών υποσυνόλων του $X$, με μετρική Hausdorff $D$. Από τη στιγμή που ο $X$ είναι πλήρης, είναι πλήρης και ο $\mathcal{K}(X)$. Ορίζουμε τη συνάρτηση $F: \mathcal{K}(X)\rightarrow \mathcal{K}(X)$ ως εξής:

$$F(A)=\bigcup_{i=1}^{n}f_i[A]$$

Η συνεχής εικόνα ενός συμπαγούς συνόλου είναι συμπαγές σύνολο (θεώρημα 1.5.6) και η ένωση πεπερασμένων συμπαγών συνόλων είναι συμπαγές. Οπότε αφού το $A$ είναι συμπαγές, τότε έχουμε ότι και το $F(A)$ είναι συμπαγές.

Ισχυριζόμαστε ότι η $F$ είναι συστολή (δηλαδή $D(F(A),F(B)\leq r D(A,B)$ με $r\in(0,1)$). Έστω

$$r=\max \{r_1,r_2,...,r_n\}$$

Προφανώς $r<1$. Πρέπει να δείξουμε ότι

$$D(F(A),F(B)\leq r D(A,B)$$ (3.8)

Έστω $q>D(A,B)$. Αν $x$ είναι οποιοδήποτε στοιχείο του $F(A)$, τότε $x=f_i(x')$ για κάποιο $i\in \{1,2,\ldots,n\}$ και $x'\in A$. Από τη στιγμή που $q>D(A,B)$, υπάρχει στοιχείο $y'\in B$ με $\rho (x',y')< q$. Τότε όμως το στοιχείο $y=f_i(y')\in F(B)$ ικανοποιεί $\rho(x,y)=r_i\rho(x',y') <r q$. Αυτό ισχύει για όλα $x\in F(A)$, άρα $F(A)$ περιέχεται στην $r q$-περιοχή του $F(B)$. Ομοίως, $F(B)$ περιέχεται στην $r q$-περιοχή του $F(A)$. Οπότε $D(F(A),F(B))\leq r q$. Αυτό ισχύει για κάθε $q>D(A,B)$, άρα έχουμε $D(F(A),F(B))\leq r D(A,B)$.

Τέλος έχουμε μια συστολή ορισμένη σε πλήρη μετρικό χώρο $\mathcal{K}(X)$. Από το θεώρημα 1.6.3 η συνάρτηση $F$ έχει μοναδικό σταθερό σημείο $K$. Το σταθερό σημείο $K=\lim_{k\rightarrow \infty}A_k$ της συνάρτησης $F$ είναι το αναλλοίωτο σύνολο στη συγκεκριμένη περίπτωση. $\Box$

Ένα από τα πλεονεκτήματα του συστήματος επαναλαμβανόμενων συναρτήσεων εφαρμοσμένων πάνω σε μια συστελλόμενη λίστα λόγου $(r_1,r_2,...,r_n)$ στο μετρικό χώρο $(X,\rho)$, είναι πως η δίασταση Hausdorff του αναλλοίωτου συνόλου σε μερικές περιπτώσεις υπολογίζεται πολύ εύκολα. Θα δείξουμε ότι υπό ορισμένες συνθήκες, η διάστση Hausdorff ενός αυτοόμοιου συνόλου $F$ είναι ίση με την τιμή του $s$ που ικανοποιεί

$$\sum_{i=1}^{n} r_i^s = 1$$ (3.9)

και επιπλέον το $F$ έχει πεπερασμένο $s$-διάστατο μέτρο Hausdorff.

Πριν προχωρήσουμε στις συνθήκες θα δείξουμε ότι το $s$ προσδιορίζεται μοναδικά.

Θεώρημα 3.4.2   Έστω $(r_1,r_2,...,r_n)$ μια συστελλόμενη λίστα λόγου (δηλαδή $r_i<1$ για όλα τα $i$). Τότε υπάρχει μοναδικός μη αρνητικός αριθμός $s$ που ικανοποιεί

$$\sum_{i=1}^{n} r_i^s = 1$$

Το $s$ είναι $0$ αν και μόνο αν $n=1$.

Απόδειξη: Θεωρούμε συνάρτηση $g:[0,\infty)\rightarrow [0,\infty)$ ορισμένη με τύπο

$$g(s)=\sum_{i=1}^{n}r_i^s$$

Τότε η $g$ είναι συνεχής, $g(0)=n \geq 1$ και $\lim_{s\rightarrow \infty}g(s)=0<1$. Άρα από το θεώρημα μέσης τιμής, υπάρχει τουλάχιστον ένα $s$ για το οποίο $g(s)=1$. Η παράγωγος της $g$ είναι

$$g'(s)=\sum_{i=1}^{n}r_i^s \log r_i$$

που είναι αρνητική ($g'(s)<0$), άρα η $g$ είναι αυστηρά φθίνουσα. Άρα υπάρχει μόνο μια λύση $s$ για την οποία $g(s)=1$. Αν το $n>1$, τότε $g(0)>1$, άρα $s\neq 0$. $\Box$

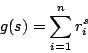
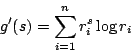
Ας δούμε τώρα ένα παράδειγμα. Θα υπολογίσουμε τη διάσταση Hausdorff για το σύνολο Cantor, $C(1/3)$, χρησιμοποιώντας τις ιδιότητες αυτοομοιότητας.

Το σύνολο Cantor $C(1/3)$ χωρίζεται σε αριστερό μέρος $C(1/3)_L=C(1/3)\cap[0,1/3]$ και δεξί μέρος $C(1/3)_R=C(1/3)\cap [2/3,1]$. Προφανώς και τα δύο μέρη είναι γεωμετρικά όμοια με το $C(1/3)$ μόνο που έχουν σμικρυνθεί κατά $1/3$ και επιπλέον $C(1/3)=C(1/3)_L\cup C(1/3)_R$ με $C(1/3)_L\cap C(1/3)_R=\emptyset$. Έτσι για $s\geq 0$ έχουμε

$$\begin{eqnarray*} \mathcal{H}^s(C(1/3))&=&\mathcal{H}^s(C(1/3)_L)+\mathcal{H}^s... ...{H}^s(C(1/3))+ \left(\frac{1}{3}\right)^s\mathcal{H}^s(C(1/3)) \end{eqnarray*}$$

από το θεώρημα 3.2.1. Αν υποθέσουμε ότι το $s$-διάστατο μέτρο Hausdorff είναι πεπερασμένο για $s=\dim_{\mathcal{H}}C(1/3)$, μπορούμε να διαιρέσουε την παραπάνω σχέση με το $\mathcal{H}^s(C(1/3))$ και θα πάρουμε $1=2(1/3)^s\Leftrightarrow s=\log 2/\log 3$

Την παραπάνω μέθοδο μερικές φορές θα τη λέμε ((ευρεστική μέθοδο)).

Οπότε αν $F=\cup_{i=1}^{n}f_i[F]$ είναι ένωση ((σχεδόν ξένων μεταξύ τους συνόλων)), έχουμε ότι

$$\mathcal{H}^s(F)=\sum_{i=1}^{n}\mathcal{H}^s(f_i[F])=\sum_{i=1}^{n}r_i^s \mathcal{H}^s(F)$$

από το θεώρημα 3.2.1. Με την υπόθεση ότι το $\mathcal{H}^s(F)$ είναι πεπερασμένο για $s=\dim_{\mathcal{H}}F$, το ζητούμενο $s$ ικανοποιεί την 3.9.

Για να είναι το αποτέλεσμα του παραπάνω επιχειρήματος σωστό, απαιτούμε να ικαναοποιείται μια συνθήκη η οποία μας εξασφαλίζει ότι τα υποσύνολα $f_i[F]$ του $F$ δεν τέμνονται ((πάρα πόλυ)).

Ορισμός 3.4.4   Λέμε ότι το σύστημα επαναλαμβανόμενων συναρτήσεων $(f_1,f_2,...,f_n)$ ικανοποιεί τη συνθήκη ανοιχτών συνόλων αν υπάρχει μη κενό φραγμένο ανοιχτό σύνολο $U$ τέτοιο ώστε

$$U\supseteq \bigcup_{i=1}^{n}f_i[U]$$

και $f_i[U]\cap f_j[U]=\emptyset$ για $i\neq j$.

Η συνθήκη λέγεται και Moran συνθήκη ανοιχτών συνόλων.

Για παράδειγμα, το σύνολο Cantor , $C(1/3)$. Το σύστημα επαναλαμβανόμενων συναρτήσεων είναι

$$\begin{eqnarray*} f_1(x)&=&\frac{x}{3}\\ f_2(x)&=&\frac{x+2}{3} \end{eqnarray*}$$

Το ανοιχτό σύνολο $(0,1)$ ικανοποιεί τη συνθήκη ανοιχτών συνόλων, αφού οι δύο εικόνες $(0,1/3)$ και $(2/3,1)$ είναι ξένες και η ένωσή τους περιέχεται στο $(0,1)$.

Θα δείξουμε ότι αν το σύστημα επαναλαμβανόμενων συναρτήσεων ικανοποιεί τη συνθήκη ανοιχτών συνόλων, τότε η διάσταση Hausdorff του αναλλοίωτου συνόλου ισούται με το $s$ που ικανοποιεί την εξίσωση 3.9.

Θα χρειαστούμε το παρακάτω γεωμετρικό αποτέλεσμα.

Λήμμα 3.4.1   Έστω $\{U_i\}$ μια συλλογή ανοιχτών ξένων μεταξύ τους υποσυνόλων του $\mathbb{R}^n$ τέτοια ώστε κάθε $U_i$ περιέχει μια ανοιχτή μπάλα ακτίνας $a_1 r$ και περιέχεται σε μια μπάλα ακτίνας $a_2 r$. Τότε οποιαδήποτε μπάλα $B$ ακτίνας $r$ τέμνει το πολύ $(1+2 a_2)^n a_1^{-n}$ κλειστοθήκες $\overline{U}_i$.

Απόδειξη: Αν $\overline{U}_i$ τέμνει $Β$, τότε το $\overline{U}_i$ περιέχεται σε μπάλα, ομοκεντρική με την $Β$ ακτίνας $(1+2a_2)r$. Υποθέτουμε ότι $q$ από τα $\overline{U}_i$ τέμνουν την $Β$. Τότε αθροίζοντας τους όγκους των αντιστοίχων εσωτερικών των μπαλών ακτίνας $a_1 r$, έχουμε ότι $q(a_1 r)^n\leq (1+2a_2)^n r^n\Rightarrow q=(1+2 a_2)^n a_1^{-n}$, που είναι και το ζητούμενο. $\Box$

Η κατασκευή (εύρεση) του κάτω φράγματος στο επόμενο θεώρημα είναι λίγο περίεργη. Ακολουθεί τη λογική που χρησιμοποιήσαμε στο παράδειγμα με τα σύνολα Cantor.

Θεώρημα 3.4.3   Έστω ότι το σύστημα επαναλαμβανόμενων συναρτήσεων $(f_1,f_2,\ldots,f_n)$ εφαρμοσμένων πάνω σε μια συστελλόμενη λίστα λόγου $(r_1,r_2,\ldots,r_n)$ στο μετρικό χώρο $(X,\rho)$, ικανοποιεί τη συνθήκη ανοιχτών συνόλων. Αν το $F$ είναι αναλλοίωτο σύνολο για το σύστημα επαναλαμβανόμενων συναρτήσεων, τότε $\dim_{\mathcal{H}}F=s$, όπου $s$ ικανοποιέι την 3.9. Επιλέον, το $s$-διάστατο μέτρο Hausdorff είναι πεπερασμένο.

Απόδειξη: Έστω $s$ ικανοποιεί την εξίσωση 3.9. Για οποιοδήποτε σύνολο $A$ γράφουμε $A_{i_1,\ldots,i_k}=f_{i_1}[f_{i_2}[\ldots[f_{i_k}[A]]]]$. Έστω $J_k$ είναι το σύνολο όλων των $κ$-οστων όρων των ακολουθιών $(i_1,\ldots,i_k)$ με $1\leq i_j\leq n$. Από την συνδύαστική ξέρουμε ότι το σύνολο $J_k$ περιέχει $n^k$ στοιχεία, από τα οποία υπάρχουν $n$ που το πρώτο τους $i$ είναι διαφορετικό, οπότε χρησιμοποιώντας το θεώρημα 1.2.1 ισχύει

$$\begin{eqnarray*} \bigcup_{J_k}F_{i_1,\ldots,i_k} &=&\bigcup_{i_1=1}^{n}f_{i_1... ...dots \left[ \bigcup_{i_k=1}^{n}f_{i_k}[F]\right]\right]\right] \end{eqnarray*}$$

Συνεπάγεται, χρησιμοποιώντας επαναληπτικά τον ορισμό του αναλλοίωτου συνόλου, ότι

$$F=\bigcup_{J_k} F_{i_1,\ldots,i_k}$$

Αυτές οι καλύψεις του $F$ μας παρέχουν το κατάλληλο άνω φράγμα για την εκτίμηση του μέτρου Hausdorff. Αφού η συνάρτηση $g(A)=f_{i_1}[f_{i_2}[\ldots[f_{i_k}[A]]]]$ είναι ομοιότητα με λόγο $(r_{i_1}r_{i_2}\cdots r_{i_k})$, θεώρημα 1.2.4, τότε

$$\sum_{J_k}(\mathop{\operator@font diam}F_{i_1,\ldots,i_k})^... ...\operator@font diam}F)^s =(\mathop{\operator@font diam}F)^s.$$

Για οποιοδήποτε $\delta>0$ μπορούμε να διαλέξουμε $k$ τέτοιο ώστε $\mathop{\operator@font diam}F_{i_1,\ldots,i_k}\leq (max_i\{r_{i_1}r_{i_2}\cdots r_{i_k}\})^k\leq \delta$, έτσι $\mathcal{H}_{\delta}^{s}(F)\leq (\mathop{\operator@font diam}F)^s$ και άρα $\mathcal{H}^s (F)\leq (\mathop{\operator@font diam}F)^s$.

Το κάτω φράγμα είναι πολύ πιο ((περιέργο)). Έστω $I$ να είναι το σύνολο όλων των άπειρων ακολουθιών $Ι=\{(i_1,i_2,\ldots)\ \hbox{όπου}\ 1\leq i_j\leq n\}$ και έστω $I_{i_1,\ldots,i_k}= \{(i_1,\ldots,i_k,q_{k+1},\ldots)\ \hbox{όπου}\ 1\leq q_j\leq n\}$ είναι η ομάδα εκείνων των $I$ τα οποία αρχίζουν με $(i_1,\ldots,i_k)$. Μπορούμε να ορίσουμε ένα πεπερασμένο μέτρο $\mathcal{M}$ στο $I$ τέτοιο ώστε $\mathcal{M}(I_{i_1,\ldots,i_k})= (r_{i_1}\cdots r_{i_k})^s$. Αφού $(r_{i_1},\ldots,r_{i_k})^s=\sum_{i=1}^{n}((r_{i_1},\ldots,r_{i_k})r_i)^s$ δηλαδή $\mathcal{M}(I_{i_1,\ldots,i_k})=\sum_{i=1}^{n}\mathcal{M}(I_{i_1,\ldots,i_k,i})$ συμπεραίνουμε ότι $\mathcal{M}$ είναι όντως μέτρο στα σύνολα του $I$ με $\mathcal{M}(I)=1$. Μπορούμε να μετατρέψουμε το $\mathcal{M}$ σε $\mathcal{N}$ στο $F$ με φυσικό τρόπο, ορίζοντας

$$\mathcal{N}(A)=\mathcal{M}(\{(i_1,i_2,\ldots)\ \hbox{όπου}\ x_{i_1},x_{i_2},\ldots\in A\})$$

για υποσύνολα $A$ του $F$. Είναι εύκολο να επιβεβαιώσουμε ότι $\mathcal{N}(F)=1$.

Θα δείξουμε ότι $\mathcal{N}$ ικανοποιεί την συνθήκη του θεωρήματος 3.3.1. Έστω $U$ να είναι ένα τέτοιο ανοιχτό σύνολο το οποίο μας εξασφαλίζει τη συνθήκη ανοιχτών συνόλων. Αφού $\overline{U}\supset\cup_{i=1}^{n}f_i[U_i]$, η ακολουθία $f^k[\overline{U}]=f_{i_1}[f_{i_2}[\ldots[f_{i_k}[\overline{U}]]]]$, όπου $1\leq i_j\leq n$, είναι φθινούσα (δηλαδή $f^0[\overline{U}]\supset f^1[\overline{U}]\supset \cdots \supset f^k[\overline{U}]$) και συγκλίνει στο $F$. Συγκεκριμένα $\overline{U}\supset F$ και $\overline{U}_{i_1,\ldots,i_k}\supset F_{i_1,\ldots,i_k}$ για κάθε πεπερασμένη ακολουθία $(i_1,\ldots,i_k)$. Έστω $B$ είναι οποιαδήποτε μπάλα με ακτίνα $r<1$.

Κόβουμε κάθε άπειρη ακολουθία $(i_1,i_2,\ldots)\in I$ μετά από τον όρο $i_k$ για το οποίο ισχύει

$$(\min_i r_i) r\leq r_{i_1},r_{i_2},\ldots,r_{i_n} \leq r$$

και ορίζουμε $Q$ να είναι πεπερασμένο σύνολο όλων των (πεπερασμένων) ακολουθιών που προκύπτουν με τον παραπάνω τρόπο. Τότε για κάθε άπειρη ακολουθία $(i_1,i_2,\ldots)\in I$ υπάρχει ακριβώς μια τιμή του $k$ με $(i_1,\ldots,i_k)\in Q$. Αφού $U_1,\ldots,U_n$ είναι ξένα μεταξύ τους, το ίδιο ισχύει και για $U_{i_1,\ldots,i_k,1},\ldots, U_{i_1,\ldots,i_k,m}$ για κάθε $(i_1,\ldots,i_k)$. Έχουμε ότι τα στοιχεία της συλλογής ανοιχτών συνόλων $\{U_{i_1,\ldots,i_k}\ \hbox{όπου}\ (i_1,\ldots,i_k)\in Q\}$ είναι ξένα μεταξύ τους. Ομοίως $F\subset \cup_Q F_{i_1,\ldots,i_k}\subset \cup_Q \overline{U}_{i_1,\ldots,i_k}$.

Διαλέγουμε $a_1$ και $a_2$ έτσι ώστε το $U$ να περιέχει μια μπάλα ακτίνας $a_1$ και να περιέχεται σε μια μπάλα ακτίνας $a_2$. Τότε για $(i_1,\ldots,i_k)\in Q$, το σύνολο $U_{i_1,\ldots,i_k}$ περιέχει μια μπάλα ακτίνας $r_{i_1}\cdots r_{i_k} a_1$, άρα και μια με ακτίνα $(\min_i r_i)r a_1$, και περιέχεται σε μια μπάλα ακτίνας $r_{i_1}\cdots r_{i_k} a_2$, άρα και σε μια με ακτίνα $r a_2$. Έστω $Q_1$ είναι το σύνολο εκείνων των ακολουθιών $(i_1,\ldots,i_k)$ του $Q$ για τις οποίες η $B$ τέμνει το $\overline{U}_{i_1,\ldots,i_k}$. Από το λήμμα 3.4.1 υπάρχουν το πολύ $q=(1+2 a_2)^n a_1^{-n}(\min_i r_i)^{-n}$ ακολουθίες στο $Q_1$. Τότε

$$\begin{eqnarray*} \mathcal{N}(B)=\mathcal{N}(F\cap B)&\leq& \mathcal{M}(\{(i_1,... ...B\})\\ &\leq&\mathcal{M}(\{\bigcup_{Q_1}I_{i_1,\ldots,i_k}\}) \end{eqnarray*}$$

αφού αν $x_{i_1},x_{i_2},\ldots \in F\cap B \subset \cup_{Q_1} \overline{U}_{i_1,\ldots,i_k}$, τότε υπάρχει ακέραιος $k$ τέτοιος ώστε $(i_1,\ldots,i_k)\in Q_1$. Έτσι

$$\begin{eqnarray*} \mathcal{N}(B)&\leq& \sum_{Q_1} \mathcal{M}(I_{i_1,\ldots,i_k... ...Q_1} (r_{i_1},\cdots,r_{i_k})^s \leq \sum_{Q_1} r^s \leq r^s q \end{eqnarray*}$$

Αφού οποιοδήποτε σύνολο $U$ περιέχεται σε μια μπάλα ακτίνας $\mathop{\operator@font diam}U$ έχουμε $\mathcal{M}(U) \leq (\mathop{\operator@font diam}U)^s q$ άρα από το θεώρημα 3.3.1 έχουμε ότι $\mathcal{H}^s(F)\geq 1/q >0$ και συνεπώς $\dim_{\mathcal{H}}F=s$ $\Box$

Figure: Τα πρώτα τρία στάδια κατασκευής του τριγώνου Sierprinsky και το ίδιο τρίγωνο Sierprinsky μετά από άπειρα βήματα. $\dim_{\mathcal{H}}S=\ln 3 /\ln 2=1,585$

Τρίγωνο Sierprinski. Θα παρουσιάσουμε τώρα την κατασκευή ενός συνόλου που θα το λέμε ((Τρίγωνο Sierprinski)), σχήμα 3.7. Ξεκινάμε με το σύνολο $S_0$ να είναι ένα ισόπλευρο τρίγωνο (μαζί με το εσωτερικό του) μήκος πλευράς 1. Το χωρίζουμε σε τέσσερα όμοια ισοσκελή τρίγωνα με μήκος πλευράς $1/2$. Το μεσαίο τρίγωνο είναι γυρισμένο κατά $180^{\circ}$ μοίρες σε σχέση με άλλα τρία. Θα αφαιρέσουμε αυτό το μεσαίο και το υπόλοιπο σύνολο θα το πούμε $S_1$. Προφανώς $S_1\subset S_0$. Τώρα κάθε ένα από τα τρία τρίγωνα που έχουν μείνει θα χωριστεί σε τέσσερα μικρότερα τρίγωνα με μήκος πλευράς $1/4$ και θα αφαιρεθούν τα τρια μεσαία. Το αποτέλεσμα θα είναι σύνολο $S_2$. Συνεχίζοντας με τον ίδιο τρόπο κατασκευάζουμε μια ακολουθία συνόλων $S_k$. Το ((τρίγωνο Sierprinski)) είναι το όριο $S$ της ακολουθίας. Μάλιστα αφού η $S_k$ είναι φθίνουσα ισχύει $S=\cap_{k=0}^{\infty}S_k$.

Το σύνολο $S_k$ αποτελείται από $3^k$ τρίγωνα με μήκος πλευράς $2^{-k}$. Άρα το συνολικό εμβαδό του $S_k$ είναι $3^k (2^{-k})^2 \sqrt{3}/4$. Αυτό συγκλίνει στο $0$ για $k\rightarrow \infty$. Οπότε το συνολικό εμβαδό του $S$ είναι $0$. Έχουμε πει ότι το δισδιάστατο μέτρο Hausdorff στο $\mathbb{R}^2$ ανιπροσωπεύει εμβαδό, αλλά και χωρίς αυτό είναι εύκολο να δούμε ότι $\mathcal{H}^2(S)=0$. Άρα η διάσταση Hausdorff του $S$ είναι μικρότερη του $2$.

Είναι εύκολο επίσης να δούμε ότι το σύνολο $S$ είναι αναλλοίωτο για το σύστημα επαναλαμβανόμενων συναρτήσεων με λίστα λόγου $\{1/2,1/2,1/2\}$ που απεικονίζει το τρίγωνο $S_0$ στα τρίγωνα του $S_1$. Αν πάρουμε το εσωτερικό του τριγώνου $S_0$, τότε αυτό είναι ανοιχτό σύνολο και ικανοποιεί τη συνθήκη ανοιχτών συνόλων. Έτσι από το θεώρημα 3.4.3, $\dim_{\mathcal{H}}S=s$ όπου $s$ ικανοποιεί την εξίσωση $\sum_{i=1}^{3}(1/2)^s=1$ δηλαδή

$$\dim_{\mathcal{H}}S=\frac{\log 3}{\log 2}$$

Καμπύλη von Koch. Έστω ότι έχουμε ένα διάστημα μήκους $h$. Θεωρούμε έναν αριθμό $a\geq 3$. Κόβουμε το μεσαίο, κομμάτι του διαστήματος μήκους $(\hbox{μήκος διαστήματος})*1/a$ και το αντικαθιστούμε με άλλα δύο διαστήματα που μαζί μ' αυτό που κόψαμε θα αποτελούσαν ένα ισόπλευρο τίγωνο. Έτσι τώρα έχουμε τέσσερα διαστήματα. Κάνουμε το ίδιο για αυτά τα τέσσερα διαστήματα. Αν συνεχίσουμε έτσι επ' άπειρο θα πάρουμε αυτό που λέμε καμπύλη von Koch σχήμα 3.8.

Το σύστημα επαναλαμβανόμενων συναρτήσεων βάσει κατασκευής αποτελείται από τέσσερις ομοιότητες $(f_1,f_2,f_3,f_4)$. Η $f_1$ συστέλει το σύνολο, διάστημα στη συγκεκριμένη περιπτωση, κατά $(a-1)/(2a)$, η $f_2$ συστέλει κατά $1/a$ περιστρέφει κατά $60^{\circ}$ και μεταφέρει κατα $(a-1)/(2α)$ μήκος και διεύθυνση του διαστήματος, η $f_3$ συστέλει κατα $1/a$ περιστέφει κατά $-60^{\circ}$ και μεταφέρει κατά $(a-1)/(2a) + 1/(2a)$ μήκος και διευθυνσή του διαστήματος και κατά $\sqrt{3}/(2a)$ στη θετική διεύθυνση της κατακόρυφης στη διεύθυνση του διαστήματος, τέλος η $f_4$ συστέλει κατά $(a-1)/(2a)$ και μεταφέρει κατά $(a-1)/(2a)+1/a$ μήκος και διεύθυνση του διαστήματος. Οπότε η λίστα λόγου μας είναι $((a-1)/(2a),1/a,1/a,(a-1)/(2a)$.

Τώρα είναι φανερό ότι η καμπύλη von Koch , $F$, είναι το αναλλοίωτο σύνολο για αυτό το σύστημα επαναλαμβανόμενων συναρτήσεων και επιπλέον ικανοποιείται η συνθήκη των ανοιχτών συνόλων αρκεί να θεωρήσουμε για ανοιχτό σύνολο το ισοσκελές τρίγωνο με βασή μήκους ένα. Μπορούμε λοιπόν να εφαρμόσουμε το θεώρημα 3.4.3 για να υπολογίσουμε την διάσταση Hausdorff: $\dim_{\mathcal{H}}F=s$ όπου το $s$ ικανοποιεί $2((1-a)/(2a))^s+2(1/a)^s=1$.

Figure: Τα πρώτα τρία στάδια της κατασκευής της καμπύλης von Koch και η ίδια καμπύλη von Koch για $a=3$. $\dim_{\mathcal{H}}F=\ln 4/\ln 3=1,262$

Το επόμενο θεώρημα, γνωστό και ως θεώρημα ((κολλάζ)), μας λέει πόσο κοντά επιτυγχάνεται η προσέγγιση που κάνουμε στο αναλλοίωτο σύνολο για το σύστημα επαναλαμβανόμενων συναρτήσεων

Θεώρημα 3.4.4   Έστω ότι έχουμε ένα σύστημα επαναλαμβανόμενων συναρτήσεων $(f_1,\ldots, f_n)$ στο $\mathbb{R}^m$ με συστελλόμενη λίστα λόγου $(r_1,\ldots,r_n)$. Έστω $E\subset \mathbb{R}^m$ ένα μη κενό συμπαγές σύνολο και $r=\max \{ r_1,\ldots,r_n\}$. Τότε

$$D(E,K)\leq D(E, \bigcup_{i=1}^{n}f_i[E])\frac{1}{1-r}$$

όπου $K$ είναι το αναλλοίωτο σύνολο για το σύστημα επαναλαμβανόμενων συναρτήσεων και $D$ είναι η μετρική Hausdorff.

Απόδειξη: Χρησιμοποιώντας την τριγωνική ανισότητα (αφού μιλάμε για μετρική) και τον ορισμό 3.4.3 του αναλλοίωτου συνόλου, έχουμε

$$\begin{eqnarray*} D(E,K)&\leq& D(E,\bigcup_{i=1}^{n}f_i[E]) + D(\bigcup_{i=1}^{... ...}^{n}f_i[K])\\ &\leq& D(E,\bigcup_{i=1}^{n}f_i[E]) + r D(E,K) \end{eqnarray*}$$

Το γεγονός ότι $D(\bigcup_{i=1}^{n}f_i[E],\bigcup_{i=1}^{n}f_i[K])\leq r D(E,K)$ το έχουμε δείξει στο θεώρημα 3.4.1, ανισότητα 3.8 $\Box$

Συμπέρασμα του παραπάνω θεωρήματος είναι ότι οποιοδήποτε συμπαγή υποσύνολο του $\mathbb{R}^n$ μπορεί να προσεγγιστεί αυθαίρετα κοντά από ένα αυτοόμοιο σύνολο. Αυτό μας λέει το επόμενο λήμμα.

Λήμμα 3.4.2   Έστω $E$ μη κενό συμπαγής υποσύνολο του $\mathbb{R}^m$. Δοθέντος $\delta>0$ υπάρχει σύστημα επαναλαμβανόμενων συναρτήσεων $f_1,\ldots,f_n$ με αναλλοίωτο σύνολο $K$ που ικανοποιεί $D(E,K)<\delta$, όπου $D$ είναι η μετρική Hausdorff.

Απόδειξη: Έστω $B_1,\ldots,B_n$ μια συλλογή μπαλών ακτίνας το πολύ $(1/4) \delta$ που καλύπτουν το $E$ και που τα κέντρα τους βρίσκονται στο $E$. Τότε $E\subset \cup_{i=1}^{n}B_i\subset N(E,\frac{1}{4}\delta)$, όπου $N(E,\frac{1}{4}\delta)$ είναι η $\delta/4$-περιοχή του $E$. Για $i=1,\ldots,n$, έστω $f_i$ να είναι συστολή με λόγο $r_i<1/2$ και πεδίο τιμών είναι $B_i$ με πεδίο ορισμού $E$. Τότε $f_i[E]\subset B_i\subset N(f_i[E],\frac{1}{2}\delta)$, έτσι $\cup_{i=1}^{n}f_i[E]\subset N(E,\frac{1}{4}\delta)$ και $E\subset \cup_{i=1}^{n}N(f_i[E],\frac{1}{2}\delta)$. Από τον ορισμό της μετρικής Hausdorff $D(E,\cup_{i=1}^{n}f_i[E])<\delta/2$. Από το θεώρημα 3.4.4 έχουμε ότι

$$D(E,K)\leq D(E,\bigcup_{i=1}^{n}f_i[E])\frac{1}{\frac{1}{2}}<\delta$$

όπου $K$ είναι το αναλλοίωτο σύνολο για το σύστημα επαναλαμβανόμενων συναρτήσεων $\Box$