




Next: Ακολουθίες
Up: Μετρική Τοπολογία
Previous: Τοπολογία Μετρικού Χώρου
Contents
Index
Ορισμός 1.2.1
Έστω 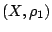
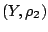 μετρικοί χώροι και μια συνάρτηση
μετρικοί χώροι και μια συνάρτηση
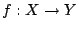 . Η
. Η  λέγεται συνεχής συνάρτηση αν
για κάθε
λέγεται συνεχής συνάρτηση αν
για κάθε 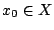 και κάθε
και κάθε
 υπάρχει
υπάρχει
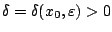 ώστε για κάθε
ώστε για κάθε  με
με
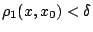 έχουμε ότι
έχουμε ότι
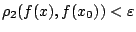 .
.
Θα ορίσουμε τώρα την συνάρτηση ομοιότητας (similarity)
Παράδειγμα:
Η ταυτοτική συνάρτηση
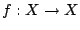 είναι συνεχής.
είναι συνεχής.
Παράδειγμα: Κάθε συνάρτηση ομοιότητας είναι συνεχής.
Απόδειξη: Αρκεί να πάρουμε
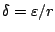 . Μάλιστα ισχύει κάτι πιο ισχυρό, κάθε συνάρτηση ομοιότητας
είναι ομοιόμορφα συνεχής.
. Μάλιστα ισχύει κάτι πιο ισχυρό, κάθε συνάρτηση ομοιότητας
είναι ομοιόμορφα συνεχής.

Ορισμός 1.2.4
Έστω
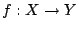 συνάρτηση και
συνάρτηση και
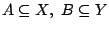 .
.
Εικόνα του  μέσω της
μέσω της  είναι
Αντίστροφη εικόνα του
είναι
Αντίστροφη εικόνα του 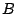 μέσω της
μέσω της  είναι
είναι
Θεώρημα 1.2.1
Έστω
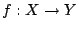 είναι μια συνάρτηση. Έστω επίσης ότι για κάθε
είναι μια συνάρτηση. Έστω επίσης ότι για κάθε 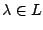 , έχουμε ότι
, έχουμε ότι
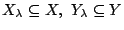 τότε
τότε
Απόδειξη: Έστω
![$y\in f[\cup_{\lambda\in L}X_{\lambda}]$](images/img234.gif) δηλαδή υπάρχει
δηλαδή υπάρχει
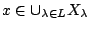 με
με 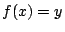 . Έχουμε
. Έχουμε
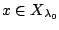 για κάποιο
για κάποιο
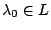 και
και 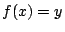 συνεπάγεται
συνεπάγεται
![$y\in f[X_{\lambda_0}]\Rightarrow y\in \cup_{\lambda\in L} f[X_{\lambda}]$](images/img239.gif) .
.
Τώρα
![$y\in \cup_{\lambda\in L}f[X_{\lambda}]\Rightarrow y\in f[X_{\lambda_0}]$](images/img240.gif) για κάποιο
για κάποιο
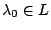 , άρα
, άρα 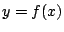 για κάποιο
για κάποιο
![$x\in X_{\lambda_0}\subseteq \cup_{\lambda\in L}X_{\lambda}\Rightarrow y\in
f[\cup_{\lambda\in L}X{\lambda}]$](images/img242.gif)

Θεώρημα 1.2.2
Έστω
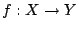 μια συνάρτηση μεταξύ μετρικών χώρων
μια συνάρτηση μεταξύ μετρικών χώρων 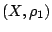 και
και 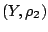 . Τότε τα
ακόλουθα είναι ισοδύναμα.
. Τότε τα
ακόλουθα είναι ισοδύναμα.
- Η
 είναι συνεχής συνάρτηση.
είναι συνεχής συνάρτηση.
- Για κάθε ανοιχτό υποσύνολο
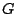 του
του  , η αντίστροφη εικόνα του
, η αντίστροφη εικόνα του 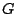 ,
, ![$f^{-1}[G]$](images/img244.gif) είναι ανοιχτό σύνολο
στο μετρικό χώρο
είναι ανοιχτό σύνολο
στο μετρικό χώρο  .
.
- Για κάθε κλειστό υποσύνολο
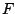 του
του  , η αντίστροφη εικόνα του
, η αντίστροφη εικόνα του 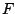 ,
, ![$f^{-1}[F]$](images/img246.gif) είναι κλειστό σύνολο
στο μετρικό χώρο
είναι κλειστό σύνολο
στο μετρικό χώρο  .
.
Απόδειξη:
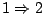 . Υποθέτουμε ότι η
. Υποθέτουμε ότι η  είναι συνεχής συνάρτηση και
είναι συνεχής συνάρτηση και 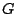 ανοιχτό σύνολο στο μετρικό
χώρο
ανοιχτό σύνολο στο μετρικό
χώρο 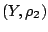 . Έστω
. Έστω
![$x_0\in f^{-1}[G]\Rightarrow f(x_0)\in G$](images/img248.gif) . Αφού το
. Αφού το 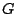 είναι ανοιχτό σύνολο,
τότε υπάρχει
είναι ανοιχτό σύνολο,
τότε υπάρχει
 ώστε
ώστε
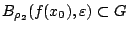 . Από την
συνέχεια της
. Από την
συνέχεια της  , υπάρχει
, υπάρχει 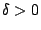 τέτοιο ώστε
τέτοιο ώστε
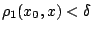 για κάθε
για κάθε
![$x\in f^{-1}[G]$](images/img252.gif) ,
δηλαδή
,
δηλαδή
![$B_{\rho_1}(x_0,\delta)\subseteq f^{-1}[G] $](images/img253.gif) . Άρα
. Άρα ![$F^{-1}[G]$](images/img254.gif) είναι ανοιχτό σύνολο στο
είναι ανοιχτό σύνολο στο  .
.
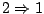 . Αντίστροφα, έστω για κάθε ανοιχτό σύνολο
. Αντίστροφα, έστω για κάθε ανοιχτό σύνολο 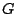 η
η ![$f^{-1}[G]$](images/img244.gif) είναι ανοιχτό και αυτό.
Θέλουμε να δείξουμε ότι η
είναι ανοιχτό και αυτό.
Θέλουμε να δείξουμε ότι η  είναι συνεχής. Έστω
είναι συνεχής. Έστω 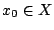 τότε για
τότε για
 η μπάλα
η μπάλα
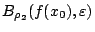 είναι ανοιχτή στο
είναι ανοιχτή στο  , άρα το σύνολο
, άρα το σύνολο
![$f^{-1}[B_{\rho_2}(f(x_0,\varepsilon )]$](images/img257.gif) είναι ανοιχτό στο
είναι ανοιχτό στο  , δηλαδή υπάρχει
, δηλαδή υπάρχει 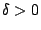 ώστε
ώστε
![$B_{\rho_1}(x_0,\delta)\subset f^{-1}[B_{\rho_2}(f(x_0),\varepsilon )]\Rightarrow \rho_1(x_0,x)<\delta $](images/img258.gif) και αφού
και αφού
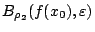 έχουμε ότι
έχουμε ότι
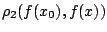 . Άρα η
. Άρα η  είναι
συνεχής συνάρτηση.
είναι
συνεχής συνάρτηση.
Τώρα
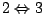 ισχύει γιατί το συμπλήρωμα του
ισχύει γιατί το συμπλήρωμα του 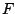 είναι ανοιχτό σύνολο και
είναι ανοιχτό σύνολο και
![$f^{-1}[F^c]=(f^{1}[F])^c$](images/img261.gif) .
.

Ορισμός 1.2.5
Έστω συνάρτηση
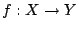 από μετρικό χώρο
από μετρικό χώρο 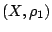 στο μετρικό χώρο
στο μετρικό χώρο 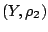 και
και
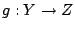 συναρτήση από το μετρικό χώρο
συναρτήση από το μετρικό χώρο 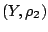 στο
στο 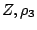 . Ορίσουμε την
σύνθεση συναρτήσεων να είναι η καινούργια συνάρτηση
. Ορίσουμε την
σύνθεση συναρτήσεων να είναι η καινούργια συνάρτηση
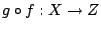 και
και
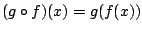 .
.
Παρατηρούμε ότι για 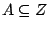 , η αντίστροφη εικόνα
, η αντίστροφη εικόνα
![$(g\circ f)^{-1}[A]=f^{-1}[g^{-1}[A]]$](images/img267.gif) .
.
Θεώρημα 1.2.3
Έστω 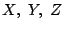 είναι μετρικοί χώροι και
είναι μετρικοί χώροι και
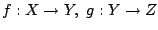 είναι δύο συνεχείς
συναρτήσεις. Τότε η σύνθεση
είναι δύο συνεχείς
συναρτήσεις. Τότε η σύνθεση 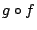 είναι και αυτή συνεχής συνάρτηση.
είναι και αυτή συνεχής συνάρτηση.
Απόδειξη: Αρκεί να δείξουμε ότι για κάθε ανοιχτό υποσύνολο  του
του 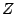 το σύνολο
το σύνολο
![$(g\circ f)^{-1}[A]$](images/img272.gif) είναι ανοιχτό
σύνολο στο
είναι ανοιχτό
σύνολο στο  . Από
το θεώρημα 1.2.2 έχουμε ότι
. Από
το θεώρημα 1.2.2 έχουμε ότι ![$g^{-1}[A]$](images/img273.gif) είναι ανοιχτό στο
είναι ανοιχτό στο  και
πάλι από
το θέωρημα 1.2.2 το
και
πάλι από
το θέωρημα 1.2.2 το
![$f^{-1}[g^{-1}[A]]$](images/img274.gif) είναι ανοιχτό σύνολο στο
είναι ανοιχτό σύνολο στο
 .
.

Θεώρημα 1.2.4
Έστω μετρικοί χώροι 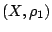 ,
, 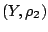 και
και 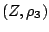 . Έστω
. Έστω
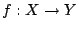 και
και
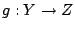 δύο ομοιότητες με λόγους
δύο ομοιότητες με λόγους 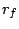 και
και 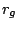 αντίστοιχα. Τότε η σύνθεση τους
αντίστοιχα. Τότε η σύνθεση τους 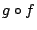 είναι ομοιότητα με λόγο
είναι ομοιότητα με λόγο
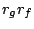 .
.
Απόδειξη:
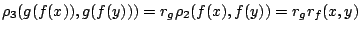






Next: Ακολουθίες
Up: Μετρική Τοπολογία
Previous: Τοπολογία Μετρικού Χώρου
Contents
Index
Khusainov Alexander
2002-10-25
![]() είναι συνεχής.
είναι συνεχής.
![]() . Μάλιστα ισχύει κάτι πιο ισχυρό, κάθε συνάρτηση ομοιότητας
είναι ομοιόμορφα συνεχής.
. Μάλιστα ισχύει κάτι πιο ισχυρό, κάθε συνάρτηση ομοιότητας
είναι ομοιόμορφα συνεχής.
![]()
![]() για κάποιο
για κάποιο
![]() , άρα
, άρα ![]() για κάποιο
για κάποιο
![]()
![]()
![]() . Αντίστροφα, έστω για κάθε ανοιχτό σύνολο
. Αντίστροφα, έστω για κάθε ανοιχτό σύνολο ![]() η
η ![]() είναι ανοιχτό και αυτό.
Θέλουμε να δείξουμε ότι η
είναι ανοιχτό και αυτό.
Θέλουμε να δείξουμε ότι η ![]() είναι συνεχής. Έστω
είναι συνεχής. Έστω ![]() τότε για
τότε για
![]() η μπάλα
η μπάλα
![]() είναι ανοιχτή στο
είναι ανοιχτή στο ![]() , άρα το σύνολο
, άρα το σύνολο
![]() είναι ανοιχτό στο
είναι ανοιχτό στο ![]() , δηλαδή υπάρχει
, δηλαδή υπάρχει ![]() ώστε
ώστε
![]() και αφού
και αφού
![]() έχουμε ότι
έχουμε ότι
![]() . Άρα η
. Άρα η ![]() είναι
συνεχής συνάρτηση.
είναι
συνεχής συνάρτηση.
![]() ισχύει γιατί το συμπλήρωμα του
ισχύει γιατί το συμπλήρωμα του ![]() είναι ανοιχτό σύνολο και
είναι ανοιχτό σύνολο και
![]() .
.
![]()
![]() , η αντίστροφη εικόνα
, η αντίστροφη εικόνα
![]() .
.