




Next: Συνεκτικοί Χώροι
Up: Μετρική Τοπολογία
Previous: Συνέχεια Συναρτήσεων
Contents
Index
Ορισμός 1.3.1
Μια συνάρτηση
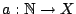 που έχει ως πεδίο ορισμού το σύνολο των φυσικών αριθμών,
λέγεται ακολουθία στο
που έχει ως πεδίο ορισμού το σύνολο των φυσικών αριθμών,
λέγεται ακολουθία στο  και συμβολίζεται με
και συμβολίζεται με 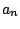 ή
ή 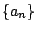 ή
ή
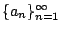 . Επιπλέον
συνηθίζουμε να γράφουμε
. Επιπλέον
συνηθίζουμε να γράφουμε 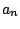 για
για 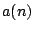 .
.
Έστω ότι έχουμε μετρικό χώρο  Λέμε ότι η ακολουθία
Λέμε ότι η ακολουθία 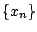 συγκλίνει
σε σημείο
συγκλίνει
σε σημείο 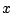 του
του  αν
για κάθε
αν
για κάθε
 , υπάρχει
, υπάρχει
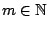 ώστε για κάθε
ώστε για κάθε 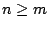
Συμβολίζουμε την σύγκλιση με
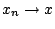 .
.
Απόδειξη: Έστω ότι η ακολουθία μας 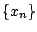 συγκλίνει και έχει δύο διαφορετικά όρια
συγκλίνει και έχει δύο διαφορετικά όρια 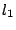 και
και 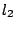 . Τότε έχουμε
ότι για
. Τότε έχουμε
ότι για
 , υπάρχει
, υπάρχει
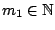 ώστε για
ώστε για 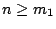 να ισχύει
να ισχύει
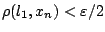 και υπάρχει
και υπάρχει
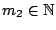 ώστε για
ώστε για 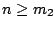 να ισχύει
να ισχύει
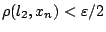 .
.
Από την τριγωνική ανισότητα έχουμε
για
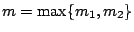 η ανισότητα γίνεται
η ανισότητα γίνεται
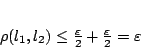 |
(1.2) |
Όμως η σχέση 1.2 ισχύει για κάθε θετικό 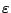 άρα
άρα
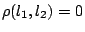 και
και 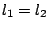 , άτοπο, δηλαδή το όριο είναι μοναδικό.
, άτοπο, δηλαδή το όριο είναι μοναδικό.

Θεώρημα 1.3.2
Έστω μετρικοί χώροι 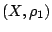 και
και 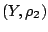 και μια συνάρτηση
και μια συνάρτηση
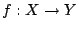 . Τότε τα
ακόλουθα είναι ισοδύναμα:
. Τότε τα
ακόλουθα είναι ισοδύναμα:
- η
 είναι συνεχής συνάρτηση.
είναι συνεχής συνάρτηση.
- αν
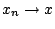 τότε
τότε
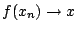
Απόδειξη:
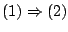 . Υποθέτουμε πρώτα ότι η
. Υποθέτουμε πρώτα ότι η  είναι συνεχής συνάρτηση και ότι
είναι συνεχής συνάρτηση και ότι
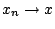 ,
θέλουμε να δείξουμε ότι
,
θέλουμε να δείξουμε ότι
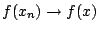 .
.
Έστω
 τότε, αφού η
τότε, αφού η  είναι συνεχής συνάρτηση, ισχύει ότι υπάρχει
είναι συνεχής συνάρτηση, ισχύει ότι υπάρχει 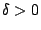 ώστε
ώστε
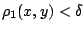 , τότε
, τότε
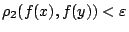 για κάθε
για κάθε 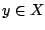 . Τώρα αφού
. Τώρα αφού
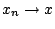 υπάρχει
υπάρχει
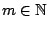 ώστε για κάθε
ώστε για κάθε 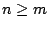 έχουμε ότι
έχουμε ότι
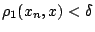 άρα
άρα
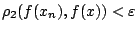 . Έτσι
. Έτσι
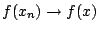 .
.
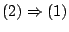 . Για
. Για  και
και
 , θα πρέπει να βρούμε
, θα πρέπει να βρούμε 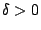 τέτοιο
ώστε
τέτοιο
ώστε
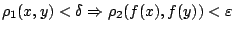 . Υποθέτουμε ότι δεν υπάρχει τέτοιο
. Υποθέτουμε ότι δεν υπάρχει τέτοιο
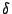 (για να καταλήξουμε σε άτοπο), αυτό σημαίνει ότι για κάθε
(για να καταλήξουμε σε άτοπο), αυτό σημαίνει ότι για κάθε
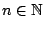 δεν ισχύει για
δεν ισχύει για
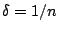 ώστε
ώστε
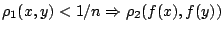 . Δηλαδή υπάρχει
. Δηλαδή υπάρχει 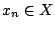 τέτοιο
ώστε
τέτοιο
ώστε
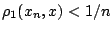 ενώ
ενώ
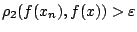 . Εξετάζουμε την ακολουθία
. Εξετάζουμε την ακολουθία 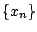 του
του  .
Έχουμε ότι
.
Έχουμε ότι
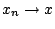 όμως
όμως
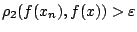 άρα
άρα 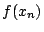 δεν συγκλίνει, άτοπο
αφού υποθέσαμε ότι
δεν συγκλίνει, άτοπο
αφού υποθέσαμε ότι
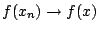 , άρα υπάρχει
, άρα υπάρχει 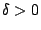 ώστε
ώστε
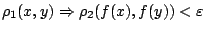 και η
και η  είναι συνεχής συνάρτηση.
είναι συνεχής συνάρτηση.

Θεώρημα 1.3.3
Η ακολουθία
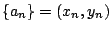 το
το 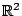 συγκλίνει στο σημείο
συγκλίνει στο σημείο
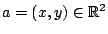 αν
και μόνο αν
αν
και μόνο αν
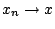 και
και
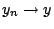 στο
στο  .
.
Θεώρημα 1.3.4
Έστω 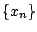 μια ακολουθία του υποσυνόλου
μια ακολουθία του υποσυνόλου  μετρικού χώρου
μετρικού χώρου  . Έστω ότι
. Έστω ότι
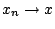 ,
τότε
,
τότε
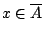 .
.
Απόδειξη: Υποθέτουμε ότι
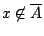 . Τότε
. Τότε
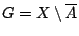 είναι ανοιχτό υποσύνολο στο
είναι ανοιχτό υποσύνολο στο  και
και 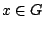 . Έχουμε ότι
. Έχουμε ότι
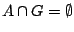 αφού
αφού
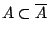 , άρα
, άρα 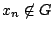 για όλα τα
για όλα τα
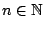 . Αφού το
. Αφού το 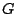 είναι ανοιχτό σύνολο έχουμε ότι για
είναι ανοιχτό σύνολο έχουμε ότι για 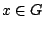 υπάρχει
υπάρχει
 με
με
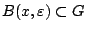 . Τώρα έχουμε ότι
. Τώρα έχουμε ότι
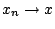 που σημαίνει ότι υπάρχει
που σημαίνει ότι υπάρχει
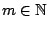 ώστε για
ώστε για 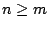 να ισχύει
να ισχύει
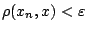 , δηλαδή από κάποιο
, δηλαδή από κάποιο 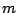 και μετά όλα τα
στοιχεία της ακολουθίας βρίσκονται στην μπάλα
και μετά όλα τα
στοιχεία της ακολουθίας βρίσκονται στην μπάλα
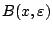 , άτοπο. Άρα
, άτοπο. Άρα
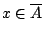 .
.

Ορισμός 1.3.2
Έστω 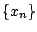 ακολουθία σημείων του μετρικού χώρου
ακολουθία σημείων του μετρικού χώρου  . Έστω
. Έστω
 όπου
όπου
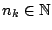 , τότε τα σημεία
, τότε τα σημεία
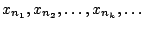 λέγεται ότι αποτελούν
υπακολουθία της
λέγεται ότι αποτελούν
υπακολουθία της  και γράφεται
και γράφεται
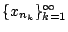 ή
ή
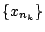 ή απλά
ή απλά 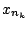 .
.
Θεώρημα 1.3.5
Έστω 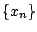 είναι μια ακολουθία μετρικού χώρου
είναι μια ακολουθία μετρικού χώρου  και έστω η ακολουθία
και έστω η ακολουθία 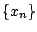 συγκλίνει στο
συγκλίνει στο
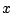 . Έστω
. Έστω
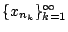 υπακολουθία της
υπακολουθία της 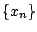 . Τότε η
. Τότε η
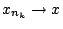 .
.
Απόδειξη: Έστω
 . Από την σύγκλιση της
. Από την σύγκλιση της  έχουμε ότι υπάρχει
έχουμε ότι υπάρχει
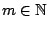 ώστε
ώστε
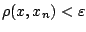 για όλα τα
για όλα τα 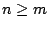 . Άρα για κάθε
. Άρα για κάθε 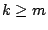 έχουμε ότι
έχουμε ότι 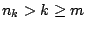 και
και
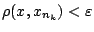 , άρα
, άρα
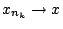 .
.






Next: Συνεκτικοί Χώροι
Up: Μετρική Τοπολογία
Previous: Συνέχεια Συναρτήσεων
Contents
Index
Khusainov Alexander
2002-10-25
![]() Λέμε ότι η ακολουθία
Λέμε ότι η ακολουθία ![]() συγκλίνει
σε σημείο
συγκλίνει
σε σημείο ![]() του
του ![]() αν
για κάθε
αν
για κάθε
![]() , υπάρχει
, υπάρχει
![]() ώστε για κάθε
ώστε για κάθε ![]()
![]() τότε, αφού η
τότε, αφού η ![]() είναι συνεχής συνάρτηση, ισχύει ότι υπάρχει
είναι συνεχής συνάρτηση, ισχύει ότι υπάρχει ![]() ώστε
ώστε
![]() , τότε
, τότε
![]() για κάθε
για κάθε ![]() . Τώρα αφού
. Τώρα αφού
![]() υπάρχει
υπάρχει
![]() ώστε για κάθε
ώστε για κάθε ![]() έχουμε ότι
έχουμε ότι
![]() άρα
άρα
![]() . Έτσι
. Έτσι
![]() .
.
![]() . Για
. Για ![]() και
και
![]() , θα πρέπει να βρούμε
, θα πρέπει να βρούμε ![]() τέτοιο
ώστε
τέτοιο
ώστε
![]() . Υποθέτουμε ότι δεν υπάρχει τέτοιο
. Υποθέτουμε ότι δεν υπάρχει τέτοιο
![]() (για να καταλήξουμε σε άτοπο), αυτό σημαίνει ότι για κάθε
(για να καταλήξουμε σε άτοπο), αυτό σημαίνει ότι για κάθε
![]() δεν ισχύει για
δεν ισχύει για
![]() ώστε
ώστε
![]() . Δηλαδή υπάρχει
. Δηλαδή υπάρχει ![]() τέτοιο
ώστε
τέτοιο
ώστε
![]() ενώ
ενώ
![]() . Εξετάζουμε την ακολουθία
. Εξετάζουμε την ακολουθία ![]() του
του ![]() .
Έχουμε ότι
.
Έχουμε ότι
![]() όμως
όμως
![]() άρα
άρα ![]() δεν συγκλίνει, άτοπο
αφού υποθέσαμε ότι
δεν συγκλίνει, άτοπο
αφού υποθέσαμε ότι
![]() , άρα υπάρχει
, άρα υπάρχει ![]() ώστε
ώστε
![]() και η
και η ![]() είναι συνεχής συνάρτηση.
είναι συνεχής συνάρτηση.
![]()