Next: Συμπάγεια
Up: Μετρική Τοπολογία
Previous: Ακολουθίες
Contents
Index
Ορισμός 1.4.1
Ένας μετρικός χώρος  λέγεται μη συνεκτικός αν υπάρχουν ανοιχτά υποσύνολα
λέγεται μη συνεκτικός αν υπάρχουν ανοιχτά υποσύνολα 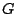 και
και 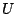 του
του  τέτοια
ώστε
τέτοια
ώστε
-
 και
και
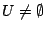
-
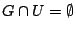
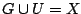
Αν δεν υπάρχουν τέτοια υποσύνολα του  , τότε ο
, τότε ο  λέγεται
συνεκτικός
λέγεται
συνεκτικός
Παράδειγμα: Ο μετρικός χώρος
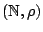 , όπου
, όπου 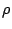 η συνήθης μετρική, είναι μη συνεκτικός, αφού
αν πάρουμε
η συνήθης μετρική, είναι μη συνεκτικός, αφού
αν πάρουμε 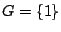 και
και
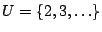 , είναι ανοιχτά στο
, είναι ανοιχτά στο
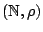 και
ικανοποιούνται οι τρεις προϋποθέσεις του ορισμού 1.4.1
και
ικανοποιούνται οι τρεις προϋποθέσεις του ορισμού 1.4.1
Μια απλή παρατήρηση: ένας μη συνεκτικός χώρος πρέπει να περιέχει τουλάχιστον δύο σημεία.
Παράδειγμα: Το κενό σύνολο όπως και τα μονοσύνολα είναι συνεκτικοί χώροι.
Λήμμα 1.4.1
Έστω
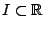 ώστε για όλα
ώστε για όλα 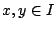 και
και 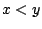 να ισχύει
να ισχύει
![$[x,y]\subset I$](images/img354.gif) τότε το
τότε το 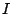 είναι
διάστημα.
είναι
διάστημα.
Απόδειξη: Θα εξετάσουμε την περίπτωση που το 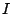 έχει άνω και κάτω πέρας (φράγμα) και δεν είναι κενό ούτε μονοσύνολο.
Έστω
έχει άνω και κάτω πέρας (φράγμα) και δεν είναι κενό ούτε μονοσύνολο.
Έστω 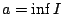 και
και 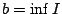 τότε
τότε 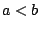 . Έστω
. Έστω 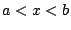 , τότε υπάρχει
, τότε υπάρχει 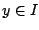 με
με 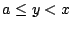 (αφού
(αφού 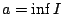 ),
ομοίως υπάρχει
),
ομοίως υπάρχει 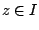 με
με 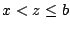 (αφού
(αφού 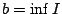 ). Από την υπόθεση
). Από την υπόθεση
![$[x,y]\subset I$](images/img354.gif) , άρα
, άρα 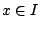 .
.
Έχουμε δείξει ότι για οποιοδήποτε 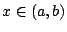 το
το 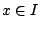 , άρα
, άρα
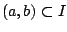 .
.
Υπάρχουν τέσσερις περιπτώσεις συνόλων με 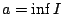 και
και 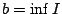 που να περιέχουν το
που να περιέχουν το 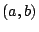 :
:
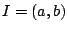 ,
, ![$I=(a,b]$](images/img370.gif) ,
, 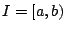 και
και ![$I=[a,b]$](images/img372.gif) . Όλες είναι διαστήματα.
. Όλες είναι διαστήματα.

Θεώρημα 1.4.1
Έστω 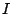 υπόχωρος του
υπόχωρος του  . Το
. Το 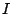 είναι συνεκτικός υπόχωρος αν και μόνο αν το
είναι συνεκτικός υπόχωρος αν και μόνο αν το 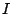 είναι διάστημα.
είναι διάστημα.
Απόδειξη: Θεωρούμε πρώτα ότι 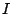 είναι διάστημα, θα δείξουμε ότι είναι συνεκτικός υπόχωρος του
είναι διάστημα, θα δείξουμε ότι είναι συνεκτικός υπόχωρος του  .
.
Υποθέτουμε ότι 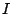 δεν είναι κενό και δεν είναι μονοσύνολο, γιατί αν ήταν, θα ήταν συνεκτικός,
οπότε θα τελείωνε η απόδειξη. Έστω λοιπόν
δεν είναι κενό και δεν είναι μονοσύνολο, γιατί αν ήταν, θα ήταν συνεκτικός,
οπότε θα τελείωνε η απόδειξη. Έστω λοιπόν 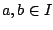 με
με 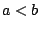 . Τότε, αφού
. Τότε, αφού  είναι διάστημα
έχουμε ότι
είναι διάστημα
έχουμε ότι
![$[a,b]\subset I$](images/img374.gif) .
.
Ας υποθέσουμε ότι υπάρχουν ανοιχτά 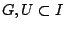 ώστε
ώστε
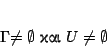 |
(1.3) |
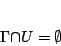 |
(1.4) |
Αρκεί να δείξουμε ότι για κάθε τέτοια δυάδα συνόλων δεν ισχύει η προϋπόθεση (3) του ορισμού 1.4.1.
Από την σχέση 1.3 έχουμε ότι υπάρχουν
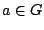 ,
, 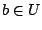 και χωρίς βλάβη της γενικότητας, έστω
και χωρίς βλάβη της γενικότητας, έστω 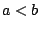 . Επειδή
. Επειδή 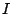 είναι διάστημα
είναι διάστημα
![$[a,b]\subset I$](images/img374.gif) .
.
Το 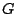 είναι ανοιχτό στο
είναι ανοιχτό στο 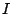 άρα αφού
άρα αφού 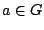 , αυτό σημαίνει ότι υπάρχει
, αυτό σημαίνει ότι υπάρχει
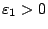 ώστε
ώστε
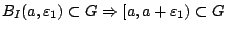 . Ανάλογα το
. Ανάλογα το 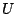 είναι ανοιχτό στο
είναι ανοιχτό στο 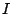 ,
,
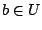 υπάρχει
υπάρχει
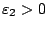 με
με
![$B_I(b,\varepsilon_2)\subset U\Rightarrow (b-\varepsilon_2,b]\subset U $](images/img383.gif) .
Θέτω
.
Θέτω
Δηλαδή
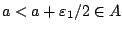 . Επειδή
. Επειδή
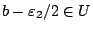 είναι άνω φράγμα του
είναι άνω φράγμα του 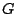 (
(
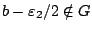 αφού
αφού
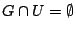 ). Άρα υπάρχει
). Άρα υπάρχει
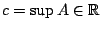 . Έχουμε
. Έχουμε
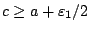 και
και
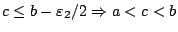 άρα
άρα 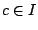 .
.
Αρκεί να δείξουμε ότι 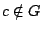 και
και 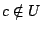 τότε θα έχουμε
τότε θα έχουμε
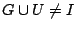 .
.
Υποθέτουμε 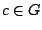 . Από την στιγμή που το
. Από την στιγμή που το 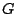 είναι ανοιχτό στο
είναι ανοιχτό στο 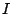 , υπάρχει
, υπάρχει  ώστε
ώστε
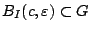 . Υποθέτουμε
. Υποθέτουμε
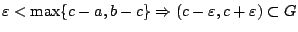 . Εφόσον
. Εφόσον
![$(c-\varepsilon, c+\varepsilon)\subset G, [a,c+\varepsilon/2]\subset G
\Rightarrow c+\varepsilon/2 \in A$](images/img398.gif) που είναι άτοπο αφού
που είναι άτοπο αφού 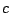 είναι άνω πέρας για το
είναι άνω πέρας για το  άρα
άρα 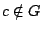 .
.
Έστω τώρα 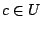 . Αφού
. Αφού 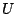 είναι ανοιχτό στο
είναι ανοιχτό στο 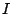 , υπάρχει
, υπάρχει  ώστε
ώστε
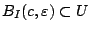 .
Μπόρουμε να υποθέσουμε ότι
.
Μπόρουμε να υποθέσουμε ότι
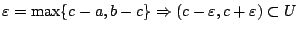 . Αφού
. Αφού
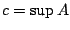 υπάρχει
υπάρχει 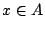 ώστε
ώστε
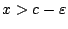 , δηλαδή
, δηλαδή
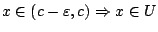 και
και
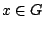 , άτοπο από την σχέση 1.4 άρα
, άτοπο από την σχέση 1.4 άρα 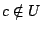 .
.
Έμεινε να δείξουμε ότι αν ο 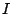 ειναι συνεκτικός τότε είναι διάστημα. Έστω ο
ειναι συνεκτικός τότε είναι διάστημα. Έστω ο 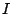 δεν είναι διάστημα αρκεί να δείξουμε ότι ο
δεν είναι διάστημα αρκεί να δείξουμε ότι ο 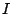 είναι μη
συνεκτικός. Από το λήμμα 1.4.1
είναι μη
συνεκτικός. Από το λήμμα 1.4.1 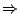 υπάρχουν
υπάρχουν 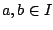 ώστε
ώστε
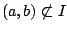 , οπότε υπάρχει
, οπότε υπάρχει 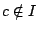 με
με 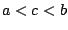 . Θέτω
. Θέτω
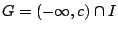 και
και
 ανοιχτά
σύνολα στο
ανοιχτά
σύνολα στο 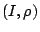 .
.
Έχουμε 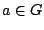 άρα
άρα
 όπως και
όπως και 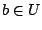 άρα
άρα
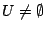 .
.
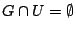 και
και
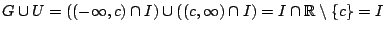 αφού
αφού 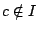 . Άρα ο
. Άρα ο 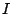 μη
συνεκτικός.
μη
συνεκτικός.

Θεώρημα 1.4.2
Έστω
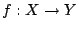 συνεχής συνάρτηση επί του
συνεχής συνάρτηση επί του  . Αν ο
. Αν ο  είναι συνεκτικός χωρος τότε και ο
είναι συνεκτικός χωρος τότε και ο  είναι
συνεκτικός.
είναι
συνεκτικός.
Απόδειξη: Υποθέτουμε ότι ο  είναι μη συνεκτικός, αρκεί να δείξουμε ότι ο
είναι μη συνεκτικός, αρκεί να δείξουμε ότι ο  δεν είναι συνεκτικός. Υπάρχουν ανοιχτά υποσύνολα
δεν είναι συνεκτικός. Υπάρχουν ανοιχτά υποσύνολα
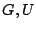 του
του  ώστε
ώστε
-
 ,
,
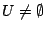
-
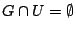
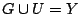
Αφού η  είναι συνεχής συνάρτηση έχουμε ότι
είναι συνεχής συνάρτηση έχουμε ότι
![$f^{-1}[G], f^{-1}[U]$](images/img416.gif) είναι ανοιχτά υποσύνολα του
είναι ανοιχτά υποσύνολα του
 , από το θεώρημα 1.2.2.
Αφού
, από το θεώρημα 1.2.2.
Αφού 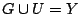 και η
και η  είναι επί, έχουμε
είναι επί, έχουμε
![$X=f^{-1}[Y]=f^{-1}[G\cup U]=f^{-1}[G]\cup f^{-1}[U]$](images/img417.gif) , δηλαδή
, δηλαδή
![\begin{displaymath}
X=f^{-1}[G]\cup f^{-1}[U]
\end{displaymath}](images/img418.gif) |
(1.5) |
Επίσης αφού
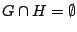 έχουμε
έχουμε
![$\emptyset=f^{-1}[\emptyset]=f^{-1}[G\cap U]$](images/img420.gif) δηλαδή
δηλαδή
![\begin{displaymath}
f^{-1}[G]\cap f^{-1}[U]=\emptyset
\end{displaymath}](images/img421.gif) |
(1.6) |
Τέλος αφού
 υπάρχει
υπάρχει 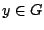 και αφού η
και αφού η  είναι επί
είναι επί 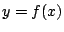 για κάποιο
για κάποιο  , μα τότε
, μα τότε
![$x\in f^{-1}[G]$](images/img252.gif) άρα
άρα
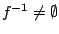 . Ομοίως
. Ομοίως
![$f^{-1}[U]\neq \emptyset$](images/img424.gif) . δηλαδή
. δηλαδή
![\begin{displaymath}
f^{-1}[G]\neq \emptyset,\ f^{-1}[U]\neq \emptyset
\end{displaymath}](images/img425.gif) |
(1.7) |
Οι 1.5, 1.6,
1.7 και το γεγονός ότι οι εικόνες ![$f^{-1}[G]$](images/img244.gif) και
και
![$f^{-1}[U]$](images/img426.gif) είναι ανοιχτά υποσύνολα του
είναι ανοιχτά υποσύνολα του  , δείχνουν ότι ο
, δείχνουν ότι ο  είναι μη συνεκτικός χώρος.
είναι μη συνεκτικός χώρος.

Παράδειγμα: Έστω
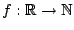 συνεχής συνάρτηση με τύπο
συνεχής συνάρτηση με τύπο 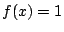 . Το
. Το  είναι συνέκτικος,
αλλά το
είναι συνέκτικος,
αλλά το 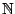 δεν είναι. Το παράδειγμα αυτό δείχνει την αναγκαιότητα η συνάρτηση
δεν είναι. Το παράδειγμα αυτό δείχνει την αναγκαιότητα η συνάρτηση  να είναι ((επί)).
να είναι ((επί)).
Πόρισμα 1.4.1
Έστω
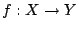 μια συνεχής συνάρτηση. Έστω ο
μια συνεχής συνάρτηση. Έστω ο  είναι συνεκτικός χώρος. Τότε η εικόνα
είναι συνεκτικός χώρος. Τότε η εικόνα
![$f[X]$](images/img430.gif) ως υπόχωρος του
ως υπόχωρος του  είναι συνεκτικός χώρος.
είναι συνεκτικός χώρος.
Πόρισμα 1.4.2
Θεώρημα Ενδιάμεσης Τιμής
Έστω
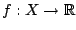 μια συνεχής συνάρτηση και ο
μια συνεχής συνάρτηση και ο  συνεκτικός χώρος. Έστω
συνεκτικός χώρος. Έστω
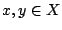 με
με 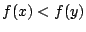 . Έστω τώρα
. Έστω τώρα
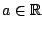 με
με 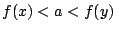 . Τότε υπάρχει
. Τότε υπάρχει
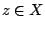 ώστε
ώστε 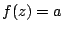 .
.
Απόδειξη: Από το πόρισμα 1.4.1 η εικόνα ![$f[X]$](images/img430.gif) είναι συνεκτικός υπόχωρος του
είναι συνεκτικός υπόχωρος του
 , άρα από το θεώρημα 1.4.1 είναι διάστημα. Τώρα
, άρα από το θεώρημα 1.4.1 είναι διάστημα. Τώρα
![$f(x),f(y)\in f[X]\Rightarrow [f(x),f(y)]\subset f[X]
\Rightarrow a\in f[X]$](images/img437.gif) υπάρχει
υπάρχει 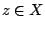 με
με 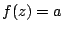

Ορισμός 1.4.2
Αν  είναι υποσύνολο ενός μετρικού χώρου
είναι υποσύνολο ενός μετρικού χώρου  , θα λέμε ότι το
, θα λέμε ότι το  είναι
συνεκτικό σύνολο αν το
είναι
συνεκτικό σύνολο αν το
 , ως υπόχωρος του μετρικού χώρου
, ως υπόχωρος του μετρικού χώρου  είναι συνεκτικός.
είναι συνεκτικός.
Ορισμός 1.4.3
Ένας υπόχωρος  του
του 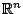 λέγεται κυρτός
αν για
λέγεται κυρτός
αν για 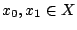 , ισχύει ότι
, ισχύει ότι
![$[x_0,x_1]\subset X$](images/img439.gif) . Όπου
. Όπου ![$[x_o,x_1]$](images/img440.gif) είναι το ευθύγραμμο
τμήμα από το
είναι το ευθύγραμμο
τμήμα από το 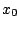 προς το
προς το 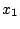 δηλαδή το σύνολο που αποτελείται από όλα τα σημεία
δηλαδή το σύνολο που αποτελείται από όλα τα σημεία
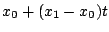 , όπου
, όπου ![$t\in [0,1]$](images/img444.gif) .
.
Παράδειγμα: Ο  είναι κυρτός
είναι κυρτός
Απόδειξη: Έστω
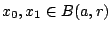 και
και ![$t\in [0,1]$](images/img444.gif) . Θέλουμε να δείξουμε ότι
. Θέλουμε να δείξουμε ότι
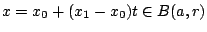 . Τώρα
. Τώρα
Άρα 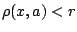 , δηλαδή
, δηλαδή 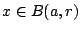 , οπότε
, οπότε 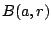 είναι κυρτό σύνολο.
είναι κυρτό σύνολο.






Next: Συμπάγεια
Up: Μετρική Τοπολογία
Previous: Ακολουθίες
Contents
Index
Khusainov Alexander
2002-10-25
 και
και
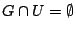
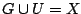
![]() το
το ![]() , άρα
, άρα
![]() .
.
![]() και
και ![]() που να περιέχουν το
που να περιέχουν το ![]() :
:
![]() ,
, ![]() ,
, ![]() και
και ![]() . Όλες είναι διαστήματα.
. Όλες είναι διαστήματα.
![]()
![]() δεν είναι κενό και δεν είναι μονοσύνολο, γιατί αν ήταν, θα ήταν συνεκτικός,
οπότε θα τελείωνε η απόδειξη. Έστω λοιπόν
δεν είναι κενό και δεν είναι μονοσύνολο, γιατί αν ήταν, θα ήταν συνεκτικός,
οπότε θα τελείωνε η απόδειξη. Έστω λοιπόν ![]() με
με ![]() . Τότε, αφού
. Τότε, αφού ![]() είναι διάστημα
έχουμε ότι
είναι διάστημα
έχουμε ότι
![]() .
.
![]() ώστε
ώστε
![]() είναι ανοιχτό στο
είναι ανοιχτό στο ![]() άρα αφού
άρα αφού ![]() , αυτό σημαίνει ότι υπάρχει
, αυτό σημαίνει ότι υπάρχει
![]() ώστε
ώστε
![]() . Ανάλογα το
. Ανάλογα το ![]() είναι ανοιχτό στο
είναι ανοιχτό στο ![]() ,
,
![]() υπάρχει
υπάρχει
![]() με
με
![]() .
Θέτω
.
Θέτω
![]() και
και ![]() τότε θα έχουμε
τότε θα έχουμε
![]() .
.
![]() . Από την στιγμή που το
. Από την στιγμή που το ![]() είναι ανοιχτό στο
είναι ανοιχτό στο ![]() , υπάρχει
, υπάρχει ![]() ώστε
ώστε
![]() . Υποθέτουμε
. Υποθέτουμε
![]() . Εφόσον
. Εφόσον
![]() που είναι άτοπο αφού
που είναι άτοπο αφού ![]() είναι άνω πέρας για το
είναι άνω πέρας για το ![]() άρα
άρα ![]() .
.
![]() . Αφού
. Αφού ![]() είναι ανοιχτό στο
είναι ανοιχτό στο ![]() , υπάρχει
, υπάρχει ![]() ώστε
ώστε
![]() .
Μπόρουμε να υποθέσουμε ότι
.
Μπόρουμε να υποθέσουμε ότι
![]() . Αφού
. Αφού
![]() υπάρχει
υπάρχει ![]() ώστε
ώστε
![]() , δηλαδή
, δηλαδή
![]() και
και
![]() , άτοπο από την σχέση 1.4 άρα
, άτοπο από την σχέση 1.4 άρα ![]() .
.
![]() ειναι συνεκτικός τότε είναι διάστημα. Έστω ο
ειναι συνεκτικός τότε είναι διάστημα. Έστω ο ![]() δεν είναι διάστημα αρκεί να δείξουμε ότι ο
δεν είναι διάστημα αρκεί να δείξουμε ότι ο ![]() είναι μη
συνεκτικός. Από το λήμμα 1.4.1
είναι μη
συνεκτικός. Από το λήμμα 1.4.1 ![]() υπάρχουν
υπάρχουν ![]() ώστε
ώστε
![]() , οπότε υπάρχει
, οπότε υπάρχει ![]() με
με ![]() . Θέτω
. Θέτω
![]() και
και
![]() ανοιχτά
σύνολα στο
ανοιχτά
σύνολα στο ![]() .
.
![]() άρα
άρα
![]() όπως και
όπως και ![]() άρα
άρα
![]() .
.
![]() και
και
![]() αφού
αφού ![]() . Άρα ο
. Άρα ο ![]() μη
συνεκτικός.
μη
συνεκτικός.
![]()