




Next: Πλήρεις και Διαχωρίσιμοι Χώροι
Up: Μετρική Τοπολογία
Previous: Συνεκτικοί Χώροι
Contents
Index
Ορισμός 1.5.1
Μια κάλυψη (ένα κάλυμμα)  ενός συνόλου
ενός συνόλου  είναι
μια συλλογή συνόλων
είναι
μια συλλογή συνόλων  ώστε
ώστε
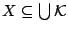 .
.
Ορισμός 1.5.2
Έστω  ένα υποσύνολο ενός μετρικού χώρου
ένα υποσύνολο ενός μετρικού χώρου  . Μια κάλυψη
. Μια κάλυψη
 του
του  ονομάζεται ανοιχτή ή
κλειστή στον
ονομάζεται ανοιχτή ή
κλειστή στον  αν καθε στοιχείο
αν καθε στοιχείο
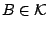 είναι ανοιχτό ή κλειστό αντίστοιχα υποσύνολα του
είναι ανοιχτό ή κλειστό αντίστοιχα υποσύνολα του  .
.
Ορισμός 1.5.3
Αν  είναι κάλυψη του μετρικού χώρου
είναι κάλυψη του μετρικού χώρου  , το υποσύνολο
, το υποσύνολο 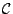 του
του  λέγεται υποκάλυψη, αν η ένωση των στοιχείων της είναι ίση με τον
λέγεται υποκάλυψη, αν η ένωση των στοιχείων της είναι ίση με τον  ,
δηλαδή αν το
,
δηλαδή αν το 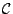 αποτελεί από μόνο του κάλυψη του
αποτελεί από μόνο του κάλυψη του 
Ορισμός 1.5.4
Ένας μετρικός χώρος  λέγεται
συμπαγής μετρικός χώρος
αν κάθε ανοιχτή κάλυψη του έχει πεπερασμένη υποκάλυψη
λέγεται
συμπαγής μετρικός χώρος
αν κάθε ανοιχτή κάλυψη του έχει πεπερασμένη υποκάλυψη
Ορισμός 1.5.5
Έστω  ένα υποσύνολο ενός μετρικού χώρου
ένα υποσύνολο ενός μετρικού χώρου  . Η
διάμετρος του
. Η
διάμετρος του
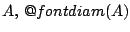 , ορίζουμε να είναι
, ορίζουμε να είναι
Απόδειξη: Υποθέτουμε ότι 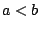 (σε αντίθετη περίπτωση
(σε αντίθετη περίπτωση 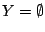 ή
ή 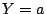 οπότε ο
οπότε ο  συμπαγής ως
πεπερασμένος).
συμπαγής ως
πεπερασμένος).
Θεωρώ ένα ανοιχτό κάλυμμα  του
του  . Υπάρχει ένα
. Υπάρχει ένα
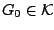 με
με 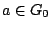 . Τώρα το
. Τώρα το 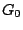 είναι ανοιχτό σύνολο του
είναι ανοιχτό σύνολο του  , δηλαδή υπάρχει
, δηλαδή υπάρχει
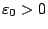 ώστε
ώστε
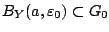 .
Ισχύει ότι
.
Ισχύει ότι
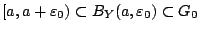 |
|
|
(1.8) |
Θέτω
![$A=\{x\in [a,b] \ \hbox{ώστε}\ [a,x]$](images/img467.gif) να περιέχεται στην ένωση μιας πεπερασμένης υποοικογένειας του
να περιέχεται στην ένωση μιας πεπερασμένης υποοικογένειας του
![$\mathcal{K} \}
=\{x\in [a,b] \ \hbox{ώστε υπάρχουν}\ G_1,G_2,\ldots,G_k\in\mat...
...\in\mathbb{N} \ \hbox{τέτοια
ώστε}\ [a,x]\subset G_1\cup G_2\cup\cdots G_k \}$](images/img468.gif)
Από την (1.8)
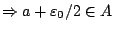 και το
και το  έχει το
έχει το 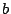 ως άνω φράγμα. Άρα
υπάρχει
ως άνω φράγμα. Άρα
υπάρχει 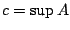 , μάλιστα
, μάλιστα
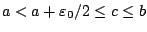
Εφόσον 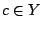 , υπάρχει
, υπάρχει
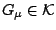 ώστε
ώστε 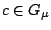 . Αφού όμως το
. Αφού όμως το 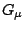 είναι
ανοιχτό σύνολο, υπάρχει
είναι
ανοιχτό σύνολο, υπάρχει 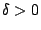 ώστε
ώστε
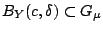 |
|
|
(1.9) |
Μπορούμε να πάρουμε 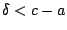 . Ας υποθέσουμε ότι
. Ας υποθέσουμε ότι 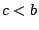 , τότε υποθέτουμε ότι
, τότε υποθέτουμε ότι
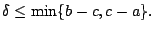
Από την (1.9)
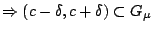 . Αφού
. Αφού 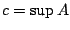 υπάρχει
υπάρχει 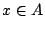 με
με
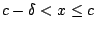 . Όμως
. Όμως
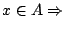 υπάρχουν
υπάρχουν
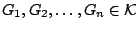 ώστε
ώστε
![$[a,x] \subset
G_1\cup G_2\cup\cdots G_n \Rightarrow [a,c+\delta / 2] \subset G_1\cup G_2 \cup\cdots G_n\cup G_{\mu}\Rightarrow
c+\delta / 2 \in A$](images/img484.gif) , άτοπο αφού
, άτοπο αφού
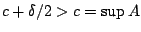 . Συμπέρασμα
. Συμπέρασμα 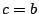 .
.
Υπάρχει δηλαδή 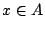 με
με 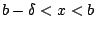 (αφού
(αφού 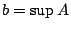 ). Άρα υπάρχει ένας πεπερασμένος αριθμός μελών του
). Άρα υπάρχει ένας πεπερασμένος αριθμός μελών του
 , έστω
, έστω
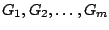 έτσι ώστε
έτσι ώστε
![$[a,x]\subset G_1\cup G_2\cup\cdots G_m$](images/img490.gif) .
.
Από την (1.9)
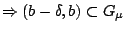 άρα
άρα
![$Y=[a,b]\subset G_1\cup G_2\cup\cdots G_m
\cup G_{\mu}\Rightarrow Y\subseteq G_1\cup G_2\cup\cdots G_{\mu}$](images/img492.gif) , άρα ο
, άρα ο  είναι συμπαγής.
είναι συμπαγής.

Ορισμός 1.5.6
Ένας μετρικός χώρος  λέγεται
φραγμένος
αν υπάρχει θετικό
λέγεται
φραγμένος
αν υπάρχει θετικό
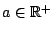 ώστε
ώστε
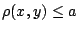 για κάθε
για κάθε 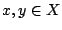
Παράδειγμα: Ένας πεπερασμένος μετρικός χώρος
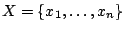 είναι φραγμένος με το φράγμα να είναι
είναι φραγμένος με το φράγμα να είναι
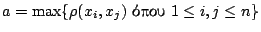 . Ένω ο μετρικός χώρος
. Ένω ο μετρικός χώρος
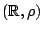 ,
όπου
,
όπου 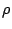 είναι συνήθης μετρική, δεν είναι φραγμένος.
είναι συνήθης μετρική, δεν είναι φραγμένος.
Πρόταση 1.5.1
Έστω  μετρικός χώρος και
μετρικός χώρος και 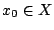 .Τότε ο
.Τότε ο  είναι φραγμένος μετρικός χώρος αν και μόνο αν
είναι φραγμένος μετρικός χώρος αν και μόνο αν
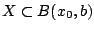 για κάποιο
για κάποιο 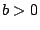 .
.
Απόδειξη: Έστω ότι ο  είναι φραγμένος, δηλαδή υπάρχει
είναι φραγμένος, δηλαδή υπάρχει 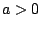 ώστε
ώστε
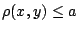 για κάθε
για κάθε 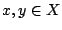 . Ισχύει
. Ισχύει
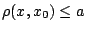 , ενώ εμείς θέλουμε
, ενώ εμείς θέλουμε 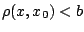 .
Αν πάρουμε
.
Αν πάρουμε 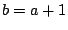 , έχουμε το ζητούμενο
, έχουμε το ζητούμενο
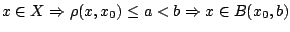 .
Δηλαδή
.
Δηλαδή
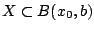 .
.
Έστω ότι
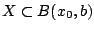 αυτό σημαίνει ότι για
αυτό σημαίνει ότι για
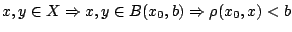 και
και
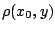 από τριγωνική ανισότητα έχουμε
από τριγωνική ανισότητα έχουμε
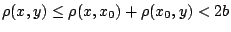 για όλα
για όλα 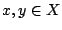 άρα ο
άρα ο
 φραγμένος.
φραγμένος.

Απόδειξη: Αν 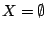 τότε είναι ήδη φραγμένος, οπότε υποθέτουμε ότι
τότε είναι ήδη φραγμένος, οπότε υποθέτουμε ότι  δεν είναι κενός, δηλαδή υπάρχει ένα
δεν είναι κενός, δηλαδή υπάρχει ένα
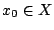 . Τώρα
. Τώρα
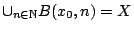 . Έστω
. Έστω  , τώρα
, τώρα
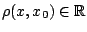 , άρα
υπάρχει
, άρα
υπάρχει
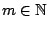 με
με
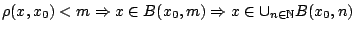 . Το αντίστροφο είναι προφανές (γιατί κάθε μπάλα είναι υποσύνολο του
. Το αντίστροφο είναι προφανές (γιατί κάθε μπάλα είναι υποσύνολο του  )
)
Έστω
 είναι ανοιχτό κάλυμμα του
είναι ανοιχτό κάλυμμα του  . Αφού
. Αφού  είναι συμπαγής
υπάρχουν
είναι συμπαγής
υπάρχουν
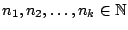 ώστε
ώστε
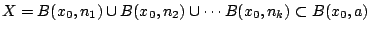 όπου
όπου
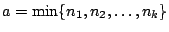 . Άρα ο
. Άρα ο  είναι φραγμένος.
είναι φραγμένος.

Θεώρημα 1.5.3
Ένας κλειστός υπόχωρος  ενός συμπαγή χώρου
ενός συμπαγή χώρου  είναι συμπαγής.
είναι συμπαγής.
Απόδειξη: Θεωρώ ανοιχτό κάλυμμα
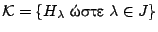 του
του  . Για κάθε
. Για κάθε
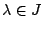 ,
, 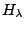 είναι ανοιχτό σύνολο του
είναι ανοιχτό σύνολο του  άρα
άρα
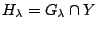 για κάποιο ανοιχτό
για κάποιο ανοιχτό
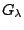 του
του  .
.  κάλυμμα του
κάλυμμα του
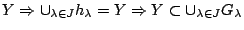 . Τώρα
. Τώρα
 είναι ανοιχτό του
είναι ανοιχτό του  και
και 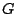 μαζί με όλα τα
μαζί με όλα τα
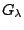 αποτελούν ανοιχτό κάλυμμα του
αποτελούν ανοιχτό κάλυμμα του  ο οποίος είναι συμπαγής. Άρα υπάρχουν
ο οποίος είναι συμπαγής. Άρα υπάρχουν
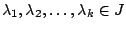 ώστε
ώστε
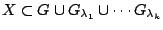 .
Τέμνοντας στην συνέχεια το
.
Τέμνοντας στην συνέχεια το  έχουμε
έχουμε
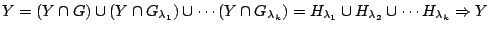 είναι συμπαγής μετρικός χώρος.
είναι συμπαγής μετρικός χώρος.

Παράδειγμα:
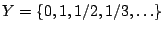 είναι κλειστό του
είναι κλειστό του ![$X=[0,1]$](images/img526.gif) άρα
άρα  είναι συμπαγής υπόχωρος του
συμπάγη χώρου
είναι συμπαγής υπόχωρος του
συμπάγη χώρου  του μετρικού χώρου
του μετρικού χώρου
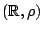 , όπου
, όπου 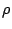 συνήθης μετρική.
συνήθης μετρική.
Θεώρημα 1.5.4
Έστω  συμπαγής υπόχωρος του
συμπαγής υπόχωρος του  . Τότε το
. Τότε το  είναι κλειστό υποσύνολο του
είναι κλειστό υποσύνολο του  .
.
Απόδειξη: Αρκεί να δείξουμε ότι ο
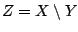 είναι ανοιχτός στον
είναι ανοιχτός στον  . Έστω
. Έστω 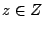 . Αρκεί να βρω
. Αρκεί να βρω
 ώστε
ώστε
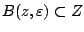 . Για κάθε
. Για κάθε 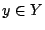 το
το 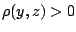 αφού
αφού 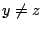 . Θέτω
. Θέτω
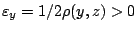 τότε
τότε
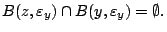 |
|
|
(1.10) |
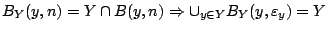 άρα
άρα
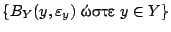 αποτελούν ανοιχτό κάλυμμα του συμπαγή χώρου
αποτελούν ανοιχτό κάλυμμα του συμπαγή χώρου  .
.
Αρά υπάρχουν
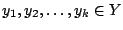 ώστε
ώστε
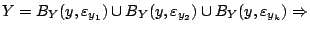
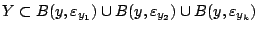 |
|
|
(1.11) |
Θέτουμε
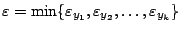
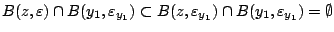 από την (1.10). Τέμνουμε την (1.10) με
από την (1.10). Τέμνουμε την (1.10) με
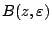 και έχουμε
και έχουμε
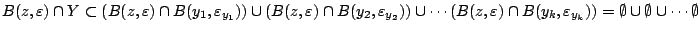 άρα
άρα
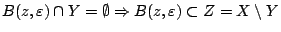 .
.

Βάσει της άρνησης ισχύει το παρακάτω πόρισμα.
Πόρισμα 1.5.1
Ένα σύνολο  που δεν είναι κλειστό στο
που δεν είναι κλειστό στο 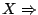 το
το  δεν είναι συμπαγής.
δεν είναι συμπαγής.
Παράδειγμα: Τα σύνολα (μετρικοί χώροι)
![$(0,1),\{1,1/2,1/3,\ldots\},(-1,0],[3,10)$](images/img546.gif) δεν είναι κλειστά στο
δεν είναι κλειστά στο  άρα δεν είναι
συμπαγείς υπόχωροι (του
άρα δεν είναι
συμπαγείς υπόχωροι (του  ). Παρατηρούμε ότι το δεύτερο σύνολο γίνεται συμπαγής αν προστεθεί το στοιχείο μηδέν.
). Παρατηρούμε ότι το δεύτερο σύνολο γίνεται συμπαγής αν προστεθεί το στοιχείο μηδέν.
Θεώρημα 1.5.5
Έστω  κλειστό και φραγμένο υποσύνολο του
κλειστό και φραγμένο υποσύνολο του  . Τότε κάθε ανοιχτή κάλυψη του
. Τότε κάθε ανοιχτή κάλυψη του  έχει πεπερασμένη υποκάλυψη, δηλαδή το
έχει πεπερασμένη υποκάλυψη, δηλαδή το  είναι συμπαγής.
είναι συμπαγής.
Απόδειξη: Έστω  κλειστό και φραγμένο σύνολο στο
κλειστό και φραγμένο σύνολο στο  . Αν
. Αν 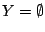 τότε είναι συμπαγής.
Μπορούμε επομένως να υποθέσουμε ότι υπάρχει
τότε είναι συμπαγής.
Μπορούμε επομένως να υποθέσουμε ότι υπάρχει 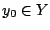 . Αφού το
. Αφού το  είναι φραγμένο, ισχύει
είναι φραγμένο, ισχύει
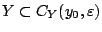 για κάποιο
για κάποιο
 , όμως
, όμως
![$C_Y(y_0,\varepsilon)\subseteq [y_0-\varepsilon,y_0+\varepsilon ]$](images/img549.gif) . Τώρα
. Τώρα
![$X=[y_0-\varepsilon,
y_0+\varepsilon]$](images/img550.gif) είναι συμπαγές σύνολο, από το θεώρημα 1.5.1. Τέλος από το θεώρημα
1.5.3 ο
είναι συμπαγές σύνολο, από το θεώρημα 1.5.1. Τέλος από το θεώρημα
1.5.3 ο  είναι κλειστός υπόχωρος συμπαγούς χώρου
είναι κλειστός υπόχωρος συμπαγούς χώρου
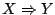 είναι συμπαγής.
είναι συμπαγής.
Έστω ότι ο χώρος  είναι συμπαγής. Τότε από το θεώρημα 1.5.2, είναι φραγμένος. Επίσης από
το θεώρημα 1.5.4, είναι και κλειστός.
είναι συμπαγής. Τότε από το θεώρημα 1.5.2, είναι φραγμένος. Επίσης από
το θεώρημα 1.5.4, είναι και κλειστός.

Στην συνέχεια θα ορίσουμε
σύνολα Cantor
στο  , τα όποια θα τα χρησιμοποιούμε σε πολλά παραδείγματα στο κεφάλαιο 3. Όπως θα
δούμε αργότερα, τα σύνολα Cantor είναι σύνολα κλασματικής διάστασης.
, τα όποια θα τα χρησιμοποιούμε σε πολλά παραδείγματα στο κεφάλαιο 3. Όπως θα
δούμε αργότερα, τα σύνολα Cantor είναι σύνολα κλασματικής διάστασης.
Έστω 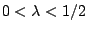 . Ορίζουμε
. Ορίζουμε ![$I_{0,1}=[0,1]$](images/img553.gif) και έστω
και έστω
![$I_{1,1}=[0,\lambda]$](images/img554.gif) και
και
![$I_{1,2}=[1-\lambda,1]$](images/img555.gif) . Συνεχίζουμε την διαδικασία διαλέγοντας υποδιαστήματα από κάθε διάστημα που
έχουμε ήδη φτιάξει. Για παράδειγμα, αν έχουμε ορίσει τα διαστήματα
. Συνεχίζουμε την διαδικασία διαλέγοντας υποδιαστήματα από κάθε διάστημα που
έχουμε ήδη φτιάξει. Για παράδειγμα, αν έχουμε ορίσει τα διαστήματα
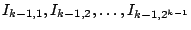 , τότε στο επόμενο βήμα ορίζουμε
, τότε στο επόμενο βήμα ορίζουμε
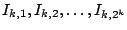 ,
διαγράφοντας από την μέση κάθε διαστήματος
,
διαγράφοντας από την μέση κάθε διαστήματος 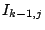 ένα διάστημα μήκους
ένα διάστημα μήκους
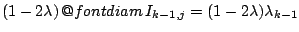 . Έτσι κάθε διάστημα
. Έτσι κάθε διάστημα 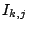 που παράγεται έχει μήκος
που παράγεται έχει μήκος 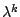 , βλέπε
σχήμα 1.1.
, βλέπε
σχήμα 1.1.
Ορισμός 1.5.7
Η οριακή κατάσταση της παραπάνω κατασκευής είναι το σύνολο Cantor με λόγο 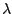
Figure:
Κατασκευή του συνόλου Cantor με λόγο
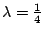 .
.
|
|
Το περισσότερο διαδεδομένο σύνολο Cantor είναι το τριαδικό, 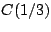
Παράδειγμα: Κάθε σύνολο Cantor με λόγο 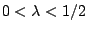 είναι συμπαγές.
είναι συμπαγές.
Απόδειξη: Το σύνολο Cantor είναι φραγμένο από 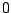 και
και 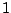 . Είναι επίσης και κλειστό ως άπειρη τομή κλειστών συνόλων. Από
το θεώρημα 1.5.5 έπεται ότι το σύνολο Cantor είναι συμπαγές.
. Είναι επίσης και κλειστό ως άπειρη τομή κλειστών συνόλων. Από
το θεώρημα 1.5.5 έπεται ότι το σύνολο Cantor είναι συμπαγές.

Οι συνεχείς συναρτήσεις μεταφέρουν την συμπάγεια, όπως συμβαίνει και με την συνεκτικότητα. Η συμπάγεια είναι
τοπολογική ιδιότητα.
Θεώρημα 1.5.6
Έστω
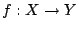 συνεχής συνάρτηση. Έστω ότι η
συνεχής συνάρτηση. Έστω ότι η  είναι επί του
είναι επί του  και ο
και ο  είναι συμπαγής. Τότε ο
είναι συμπαγής. Τότε ο
 είναι συμπαγής.
είναι συμπαγής.
Απόδειξη: Έστω
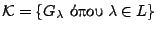 είναι ανοιχτή κάλυψη του
είναι ανοιχτή κάλυψη του  . Για κάθε
. Για κάθε
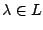 το σύνολο
το σύνολο
![$H_{\lambda}=f^{-1}[G_{\lambda}]$](images/img566.gif) είναι ανοιχτό του
είναι ανοιχτό του  , αφού η
, αφού η  είναι συνεχής.
Επίσης
είναι συνεχής.
Επίσης
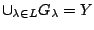 . Άρα
. Άρα
![$X=f^{-1}[Y]=\cup_{\lambda \in L}f^{-1}[G_{\lambda}]$](images/img568.gif) . Έτσι
το
. Έτσι
το
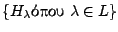 είναι ανοιχτή κάλυψη του
είναι ανοιχτή κάλυψη του  . Ο
. Ο  όμως είναι συμπαγής, άρα
υπάρχουν
όμως είναι συμπαγής, άρα
υπάρχουν
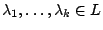 με
με
![$X=H_{\lambda_1}\cup\cdots\cup H_{\lambda_k}\Rightarrow
f[X]=f[H_{\lambda_1}]\cup\cdots\cup f[H_{\lambda_k}]$](images/img571.gif) . Τώρα, αφού η
. Τώρα, αφού η  είναι επί του
είναι επί του  ισχύει
ισχύει ![$f[X]=Y$](images/img572.gif) , άρα
έχουμε
, άρα
έχουμε
![$Y=f^{-1}[H_{\lambda_1}]\cup\cdots\cup f^{-1}[H_{\lambda_k}]=f[f^{-1}[G_{\lambda_1}]]\cup\cdots\cup
f[f^{-1}[G_{\lambda_k}]]=G_{}\cup\cdots\cup G_{}$](images/img573.gif) .
.
Άρα ο  είναι συμπαγής.
είναι συμπαγής.

Πόρισμα 1.5.2
Έστω
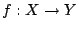 είναι συνεχής συνάρτηση, όπου
είναι συνεχής συνάρτηση, όπου  είναι συμπαγής μετρικός χώρος. Τότε ο υπόχωρος
είναι συμπαγής μετρικός χώρος. Τότε ο υπόχωρος ![$f[X]$](images/img430.gif) του
του  είναι συμπαγής
είναι συμπαγής
Πόρισμα 1.5.3
Έστω ο  συμπαγής, μη κενός μετρικός χώρος. Έστω η
συμπαγής, μη κενός μετρικός χώρος. Έστω η
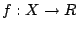 μια συνεχής συνάρτηση. Τότε η
μια συνεχής συνάρτηση. Τότε η
 είναι φραγμένη και λαμβάνει ελάχιστη και μέγιστη τιμή.
είναι φραγμένη και λαμβάνει ελάχιστη και μέγιστη τιμή.
Απόδειξη: Το σύνολο ![$f[X]$](images/img430.gif) είναι συμπαγής υπόχωρος του
είναι συμπαγής υπόχωρος του  , από το πόρισμα 1.5.2.
Άρα το
, από το πόρισμα 1.5.2.
Άρα το ![$f[X]$](images/img430.gif) είναι κλειστό και φραγμένο σύνολο. Εφόσον το
είναι κλειστό και φραγμένο σύνολο. Εφόσον το  είναι μη κενό, θα έχει άνω και κάτω φράγμα, δηλαδή
θα υπάρχει
είναι μη κενό, θα έχει άνω και κάτω φράγμα, δηλαδή
θα υπάρχει
![$a=\inf\{f[X]\}$](images/img575.gif) και
και
![$b=\sup\{f[X]\}$](images/img576.gif) όπου
όπου
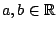 . Τώρα για κάθε
. Τώρα για κάθε
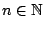 έχουμε
έχουμε  συνεπάγεται ότι υπάρχει
συνεπάγεται ότι υπάρχει ![$y_n\in f[X]$](images/img578.gif) με
με 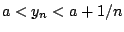 (ορισμός
του κάτω πέρατος). Τότε
(ορισμός
του κάτω πέρατος). Τότε
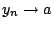 . Επειδή
. Επειδή ![$y_n\in f[X]$](images/img578.gif) έχουμε
έχουμε ![$a\in f[X]$](images/img581.gif) , αφού το
, αφού το ![$f[X]$](images/img430.gif) είναι κλειστό.
Άρα για κάποιο
είναι κλειστό.
Άρα για κάποιο 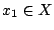 έχουμε
έχουμε 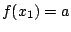 . Τώρα για κάθε
. Τώρα για κάθε  έχουμε
έχουμε ![$f(x)\in f[X])$](images/img584.gif) . Δηλαδή
. Δηλαδή
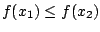 για κάθε
για κάθε  , άρα η
, άρα η  έχει ελάχιστη τιμή
έχει ελάχιστη τιμή 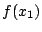
Ομοίως αποδεικνύουμε για μέγιστή τιμή.

Ορισμός 1.5.8
Έστω  μετρικός χώρος. Ο
μετρικός χώρος. Ο  λέγεται ακολουθιακά συμπαγής αν κάθε ακολουθία του έχει συγκλίνουσα
υπακολουθία.
λέγεται ακολουθιακά συμπαγής αν κάθε ακολουθία του έχει συγκλίνουσα
υπακολουθία.
Ορισμός 1.5.9
Έστω  μετρικός χώρος. Ο
μετρικός χώρος. Ο  έχει την ιδιότητα Bolzano - Weierstrass αν κάθε άπειρο υποσύνολο
έχει την ιδιότητα Bolzano - Weierstrass αν κάθε άπειρο υποσύνολο
 του
του  έχει τουλάχιστον ένα σημείο συσσώρευσης, ή ισοδύναμα αν το παράγωγο σύνολο του
έχει τουλάχιστον ένα σημείο συσσώρευσης, ή ισοδύναμα αν το παράγωγο σύνολο του  είναι
μη κενό (
είναι
μη κενό (
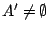 )
)
Θεώρημα 1.5.7
Θεώρημα Lebesgue
Έστω  ακολουθιακά συμπαγής μετρικός χώρος. Έστω
ακολουθιακά συμπαγής μετρικός χώρος. Έστω  είναι μια ανοιχτή κάλυψη του
είναι μια ανοιχτή κάλυψη του  .
Τότε υπάρχει
.
Τότε υπάρχει  ώστε για κάθε
ώστε για κάθε  , η ανοιχτή μπάλα
, η ανοιχτή μπάλα
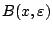 να περιέχεται σε
κάποιο από τα στοιχεία της
να περιέχεται σε
κάποιο από τα στοιχεία της  .
.
Απόδειξη: Υποθέτουμε ότι δεν υπάρχει τέτοιο 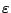 (για να καταλήξουμε σε άτοπο). Τότε για κάθε
(για να καταλήξουμε σε άτοπο). Τότε για κάθε
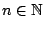 το
το
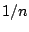 δεν έχει την παραπάνω ιδιότητα, δηλαδή υπάρχει
δεν έχει την παραπάνω ιδιότητα, δηλαδή υπάρχει 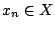 ώστε
ώστε 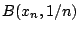 δεν περιέχεται σε κανένα
από τα στοιχεία της
δεν περιέχεται σε κανένα
από τα στοιχεία της  .
.
Αφού ο  είναι ακολουθιακά συμπαγής, υπάρχει μια υπακολουθία
είναι ακολουθιακά συμπαγής, υπάρχει μια υπακολουθία 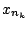 της
της  η οποία συγκλίνει σε κάποιο
σημείο
η οποία συγκλίνει σε κάποιο
σημείο 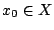 . Εφόσον η
. Εφόσον η  είναι ανοιχτή κάλυψη, υπάρχει
είναι ανοιχτή κάλυψη, υπάρχει
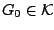 ώστε
ώστε
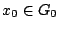 . Αφού
. Αφού 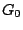 ανοιχτό, υπάρχει
ανοιχτό, υπάρχει  ώστε
ώστε
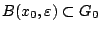 . Επιπλέον
. Επιπλέον
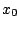 είναι όριο της ακολουθίας
είναι όριο της ακολουθίας 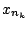 , άρα από κάποιο
, άρα από κάποιο 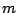 και μετά όλα τα στοιχεία της
και μετά όλα τα στοιχεία της 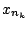 θα
βρίσκονται στην ανοιχτή μπάλα
θα
βρίσκονται στην ανοιχτή μπάλα
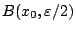 , δηλαδή
, δηλαδή
Άρα υπάρχει κάποιο 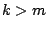 (πολύ μεγάλο) με
(πολύ μεγάλο) με
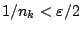 και
και
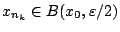 . Τώρα
. Τώρα
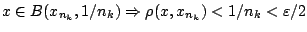 και από τριγωνική ανισότητα
και από τριγωνική ανισότητα
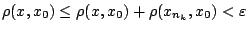 δηλαδή
δηλαδή
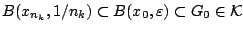 που είναι άτοπο.
που είναι άτοπο.

Θεώρημα 1.5.8
Έστω  μετρικός χώρος. Τα ακόλουθα είναι ισοδύναμα:
μετρικός χώρος. Τα ακόλουθα είναι ισοδύναμα:
- ο
 είναι συμπαγής
είναι συμπαγής
- ο
 έχει την ιδιότητα Bolzano - Weierstrass
έχει την ιδιότητα Bolzano - Weierstrass
- ο
 είναι ακολουθιακά συμπαγής
είναι ακολουθιακά συμπαγής
Απόδειξη:
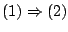 . Έστω
. Έστω  άπειρο υποσύνολο του
άπειρο υποσύνολο του  . Αρκεί να δείξουμε ότι
. Αρκεί να δείξουμε ότι
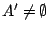 . Υποθέτουμε ότι
. Υποθέτουμε ότι
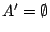 (για να καταλήξουμε σε άτοπο). Αφού το
(για να καταλήξουμε σε άτοπο). Αφού το  είναι άπειρο, το
είναι άπειρο, το  περιέχει διακεκριμένα σημεία
περιέχει διακεκριμένα σημεία
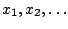 . Τώρα
. Τώρα
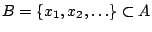 , άρα
, άρα
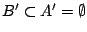 , δηλαδή το παράγωγο του
, δηλαδή το παράγωγο του 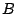 είναι κενό, συμπεραίνουμε επίσης ότι το
είναι κενό, συμπεραίνουμε επίσης ότι το 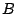 είναι κλειστό αφού
είναι κλειστό αφού
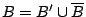 . Επίσης από την υπόθεση
έχουμε ότι ο
. Επίσης από την υπόθεση
έχουμε ότι ο  είναι συμπαγής. Από το θεώρημα 1.5.3 ο
είναι συμπαγής. Από το θεώρημα 1.5.3 ο 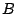 είναι και αυτός συμπαγής
υπόχωρος του
είναι και αυτός συμπαγής
υπόχωρος του  .
.
Τώρα κάθε μονοσύνολο
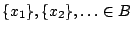 είναι ανοιχτό υποσύνολο του
είναι ανοιχτό υποσύνολο του 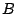 και
και
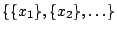 είναι ανοιχτή κάλυψη του
είναι ανοιχτή κάλυψη του 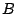 , η οποία δεν έχει πεπερασμένη ανοιχτή υποκάλυψη, γιατι τα
, η οποία δεν έχει πεπερασμένη ανοιχτή υποκάλυψη, γιατι τα
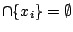 , άρα
ο
, άρα
ο 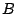 δεν είναι συμπαγής, που είναι άτοπο, άρα
δεν είναι συμπαγής, που είναι άτοπο, άρα
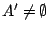 και ο
και ο  έχει την ιδιότητα Bolzano - Weierstrass.
έχει την ιδιότητα Bolzano - Weierstrass.
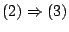 Έστω τώρα ότι ο
Έστω τώρα ότι ο  έχει την ιδιότητα Bolzano - Weirstrass. Θεωρούμε την ακολουθία
έχει την ιδιότητα Bolzano - Weirstrass. Θεωρούμε την ακολουθία
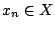 , θέλουμε να δείξουμε ότι η
, θέλουμε να δείξουμε ότι η  έχει συγκλίνουσα υπακολουθία.
έχει συγκλίνουσα υπακολουθία.
Ας εξετάσουμε το σύνολο
Υπάρχουν δύο περιπτώσεις, είτε το  είναι πεπερασμένο, είτε αριθμήσιμο άπειρο.
είναι πεπερασμένο, είτε αριθμήσιμο άπειρο.
Αν το  έχει πεπερασμένο το πλήθος στοιχείων, δηλαδή
έχει πεπερασμένο το πλήθος στοιχείων, δηλαδή
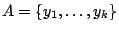 . Θέτουμε
. Θέτουμε
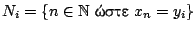 τότε
τότε
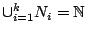 . Τουλάχιστον ένα από τα
. Τουλάχιστον ένα από τα
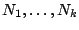 είναι
αριθμήσιμα άπειρο. Υποθέτουμε χωρίς βλάβη της γενικότητας ότι
είναι
αριθμήσιμα άπειρο. Υποθέτουμε χωρίς βλάβη της γενικότητας ότι 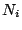 έχει άπειρα στοιχεία
έχει άπειρα στοιχεία
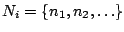 όπου
όπου
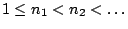 . Για κάθε
. Για κάθε
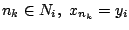 , άρα
, άρα
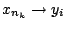 . Οπότε υπάρχει
συγκλίνουσα υπακολουθία της
. Οπότε υπάρχει
συγκλίνουσα υπακολουθία της  που έχει όριο στο
που έχει όριο στο  .
.
Αν τώρα  έχει αριθμήσιμο άπειρο το πλήθος στοιχείων, από τον ορισμό της ιδιότητας Bolzano -
Weierstrass, έχουμε ότι
έχει αριθμήσιμο άπειρο το πλήθος στοιχείων, από τον ορισμό της ιδιότητας Bolzano -
Weierstrass, έχουμε ότι
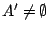 . Άρα υπάρχει
. Άρα υπάρχει 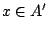 .
Κατασκευάζουμε στην συνέχεια την υπακολουθία μας
.
Κατασκευάζουμε στην συνέχεια την υπακολουθία μας
Τώρα 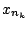 είναι υπακολουθία της
είναι υπακολουθία της  και
και
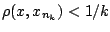 , άρα
, άρα
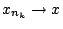 .
.
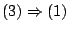 Έστω τώρα
Έστω τώρα  ακολουθιακά συμπαγής, θέλουμε να δείξουμε ότι είναι συμπαγής. Θεωρούμε ανοιχτή κάληψη
ακολουθιακά συμπαγής, θέλουμε να δείξουμε ότι είναι συμπαγής. Θεωρούμε ανοιχτή κάληψη
 του
του  . Υποθέτουμε ότι η
. Υποθέτουμε ότι η  δεν έχει πεπερασμένη υποκάλυψη (για να καταλήξουμε σε
άτοπο).
δεν έχει πεπερασμένη υποκάλυψη (για να καταλήξουμε σε
άτοπο).
Από το θεώρημα 1.5.7 υπάρχει  ώστε
ώστε
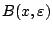 να περιέχεται σε
κάποιο μέλος της
να περιέχεται σε
κάποιο μέλος της  για κάθε
για κάθε  . Οπότε υπάρχει
. Οπότε υπάρχει 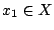 και
και
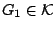 με
με
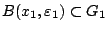 , υπάρχει επίσης
, υπάρχει επίσης
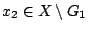 και
και
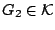 ώστε
ώστε
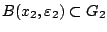 . Τώρα έχουμε θεωρήσει πως
. Τώρα έχουμε θεωρήσει πως  δεν έχει πεπερασμένη υπόκαλυψη,
άρα
δεν έχει πεπερασμένη υπόκαλυψη,
άρα
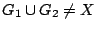 . Άρα υπάρχει
. Άρα υπάρχει
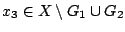 και
και
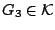 με
με
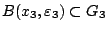 . Συνεχίζουμε έτσι και κατασκευάζουμε την ακολουθία
. Συνεχίζουμε έτσι και κατασκευάζουμε την ακολουθία
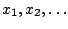 , με
, με
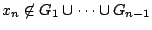 και να υπάρχει σύνολο
και να υπάρχει σύνολο
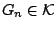 ώστε
ώστε
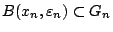 .
.
Έτσι για τυχόντα 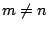 ισχύει
ισχύει
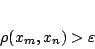 |
(1.12) |
Εφόσον ο χώρος  είναι ακολουθιακά συμπαγής υπάρχει υπακολουθία
είναι ακολουθιακά συμπαγής υπάρχει υπακολουθία 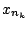 της
της  που συγκλίνει σε
σημείο
που συγκλίνει σε
σημείο 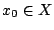 . Αφού
. Αφού
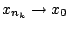 μπορούμε να συμπεραίνουμε ότι υπάρχουν τουλάχιστον δύο
υπακολουθίες
μπορούμε να συμπεραίνουμε ότι υπάρχουν τουλάχιστον δύο
υπακολουθίες 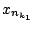 και
και 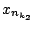 με
με
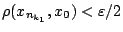 και
και
 . Τότε από τριγωνική ανισότητα έχουμε
. Τότε από τριγωνική ανισότητα έχουμε
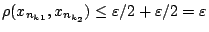 που αντιφάσκει με την 1.12. Άτοπο.
που αντιφάσκει με την 1.12. Άτοπο.

Θεώρημα 1.5.9
Έστω 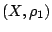 και
και 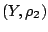 είναι μετρικοί χώροι. Έστω ότι ο
είναι μετρικοί χώροι. Έστω ότι ο  είναι συμπαγής χώρος. Τότε
κάθε συνεχής συνάρτηση
είναι συμπαγής χώρος. Τότε
κάθε συνεχής συνάρτηση
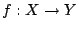 είναι ομοιόμορφα συνεχής.
είναι ομοιόμορφα συνεχής.
Απόδειξη: Έστω  θέλουμε
θέλουμε 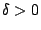 ώστε
ώστε
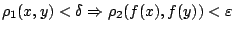 .
Θεωρούμε όλες τις μπάλες
.
Θεωρούμε όλες τις μπάλες
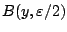 του
του 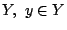 . Τότε
. Τότε
![$f^{-1}[B(y,\varepsilon/2)]$](images/img647.gif) είναι
ανοιχτό του
είναι
ανοιχτό του  , γιατί η
, γιατί η  είναι συνεχής συνάρτηση.
είναι συνεχής συνάρτηση.
Τώρα
![$\mathcal{K}=\{f^{-1}[B(y,\varepsilon/2)]\ \hbox{όπου}\ y\in Y\}$](images/img648.gif) είναι ανοιχτή κάλυψη του συμπαγούς
είναι ανοιχτή κάλυψη του συμπαγούς
 . Από το θεώρημα 1.5.7 υπάρχει
. Από το θεώρημα 1.5.7 υπάρχει 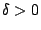 ώστε για κάθε
ώστε για κάθε  η μπάλα
η μπάλα
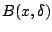 να περιέχεται σε κάποιο στοιχείο της
να περιέχεται σε κάποιο στοιχείο της  . Έστω ότι
. Έστω ότι
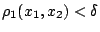 , τότε
, τότε
![$x_2\in B(x_1,\delta)\Rightarrow B(x_1,\delta)\subset f^{-1}[B(y,\varepsilon/2)]$](images/img651.gif) για κάποιο
για κάποιο 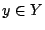 . Αφού
. Αφού
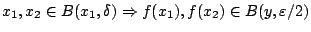 και από τριγωνική ανισότητα
και από τριγωνική ανισότητα
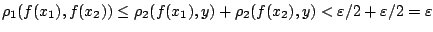 .
Άρα αν
.
Άρα αν
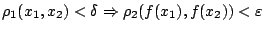 .
.
Άρα η  είναι ομοιόμορφα συνεχής.
είναι ομοιόμορφα συνεχής.

Θεώρημα 1.5.10
Έστω  υπόχωρος του
υπόχωρος του 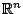 τότε ο
τότε ο  είναι συμπαγής αν και μόνο αν ο
είναι συμπαγής αν και μόνο αν ο  είναι κλειστός και
φραγμένος στο
είναι κλειστός και
φραγμένος στο 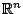 .
.
Απόδειξη: Αν ο  συμπαγής υπόχωρος του
συμπαγής υπόχωρος του 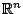 , τότε από το θεώρημα 1.5.2 είναι φραγμένος και
από το θεώρημα 1.5.4 είναι κλειστός.
, τότε από το θεώρημα 1.5.2 είναι φραγμένος και
από το θεώρημα 1.5.4 είναι κλειστός.
Τώρα αν ο  είναι κλειστός και φραγμένος υπόχωρος του
είναι κλειστός και φραγμένος υπόχωρος του 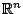 θέλουμε να δείξουμε ότι ο
θέλουμε να δείξουμε ότι ο  είναι
συμπαγής. Αρκεί να δείξουμε ότι είναι ακολουθιακά συμπαγής. Θα το δείξουμε για
είναι
συμπαγής. Αρκεί να δείξουμε ότι είναι ακολουθιακά συμπαγής. Θα το δείξουμε για 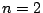 , δηλαδή
, δηλαδή
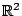 , αφού η απόδειξη για οποιοδήποτε
, αφού η απόδειξη για οποιοδήποτε 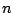 είναι παρόμοια (αλλά ίσως πιο πολύπλοκη).
είναι παρόμοια (αλλά ίσως πιο πολύπλοκη).
Εξετάζω την ακολουθία
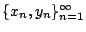 του
του  . Αφού ο
. Αφού ο  είναι φραγμένος, υπάρχει κάποιο
είναι φραγμένος, υπάρχει κάποιο
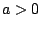 ώστε
ώστε 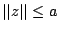 για όλα τα
για όλα τα
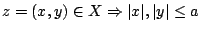 . Έτσι για κάθε
. Έτσι για κάθε
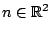 έχουμε
έχουμε
![$x_n,y_n \in [-a,a]$](images/img660.gif) , οπότε
, οπότε 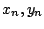 είναι ακολουθίες στο συμπαγές
είναι ακολουθίες στο συμπαγές ![$[-a,a]$](images/img662.gif) .
Άρα υπάρχει υπακολουθία
.
Άρα υπάρχει υπακολουθία 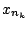 της
της  που να συγκλίνει σε σημείο
που να συγκλίνει σε σημείο 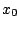 του
του ![$[-a,a]$](images/img662.gif) . Τώρα για το
ίδιο λόγο η ακολουθία
. Τώρα για το
ίδιο λόγο η ακολουθία 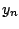 έχει συγκλίνουσα υπακολουθία
έχει συγκλίνουσα υπακολουθία 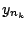 , όριο της οποίας είναι
, όριο της οποίας είναι ![$y_0\in [-a,a]$](images/img665.gif) .
.
Τώρα έχουμε
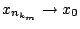 και
και
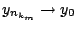 , από το θεώρημα
1.3.3
, από το θεώρημα
1.3.3
Επειδή
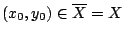 , έχουμε ότι η υπακολουθία
, έχουμε ότι η υπακολουθία
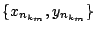 της
της
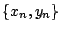 συγκλίνει σε σημείο του
συγκλίνει σε σημείο του  , άρα ο
, άρα ο  είναι ακολουθιακά συμπαγής.
είναι ακολουθιακά συμπαγής.

Απόδειξη: Έστω
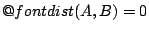 . Τότε υπάρχει σημείο
. Τότε υπάρχει σημείο 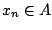 και
και 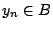 με
με
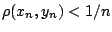 . Τώρα ο
. Τώρα ο 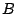 είναι συμπαγης, άρα (αντικαθιστώντας την ακολουθίες με υπακολουθίες) μπορούμε να υποθέσουμε ότι
είναι συμπαγης, άρα (αντικαθιστώντας την ακολουθίες με υπακολουθίες) μπορούμε να υποθέσουμε ότι
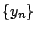 συγκλίνει. Έστω
συγκλίνει. Έστω
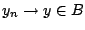 . Τότε
. Τότε
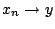 επίσης. Όμως το
επίσης. Όμως το  είναι κλειστό σύνολο, άρα
είναι κλειστό σύνολο, άρα 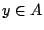 . Οπότε
. Οπότε
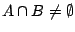 .
.






Next: Πλήρεις και Διαχωρίσιμοι Χώροι
Up: Μετρική Τοπολογία
Previous: Συνεκτικοί Χώροι
Contents
Index
Khusainov Alexander
2002-10-25
![]() του
του ![]() . Υπάρχει ένα
. Υπάρχει ένα
![]() με
με ![]() . Τώρα το
. Τώρα το ![]() είναι ανοιχτό σύνολο του
είναι ανοιχτό σύνολο του ![]() , δηλαδή υπάρχει
, δηλαδή υπάρχει
![]() ώστε
ώστε
![]() .
Ισχύει ότι
.
Ισχύει ότι
![]() και το
και το ![]() έχει το
έχει το ![]() ως άνω φράγμα. Άρα
υπάρχει
ως άνω φράγμα. Άρα
υπάρχει ![]() , μάλιστα
, μάλιστα
![]()
![]() , υπάρχει
, υπάρχει
![]() ώστε
ώστε ![]() . Αφού όμως το
. Αφού όμως το ![]() είναι
ανοιχτό σύνολο, υπάρχει
είναι
ανοιχτό σύνολο, υπάρχει ![]() ώστε
ώστε
![]() . Αφού
. Αφού ![]() υπάρχει
υπάρχει ![]() με
με
![]() . Όμως
. Όμως
![]() υπάρχουν
υπάρχουν
![]() ώστε
ώστε
![]() , άτοπο αφού
, άτοπο αφού
![]() . Συμπέρασμα
. Συμπέρασμα ![]() .
.
![]() με
με ![]() (αφού
(αφού ![]() ). Άρα υπάρχει ένας πεπερασμένος αριθμός μελών του
). Άρα υπάρχει ένας πεπερασμένος αριθμός μελών του
![]() , έστω
, έστω
![]() έτσι ώστε
έτσι ώστε
![]() .
.
![]() άρα
άρα
![]() , άρα ο
, άρα ο ![]() είναι συμπαγής.
είναι συμπαγής.
![]()
![]() είναι φραγμένος με το φράγμα να είναι
είναι φραγμένος με το φράγμα να είναι
![]() . Ένω ο μετρικός χώρος
. Ένω ο μετρικός χώρος
![]() ,
όπου
,
όπου ![]() είναι συνήθης μετρική, δεν είναι φραγμένος.
είναι συνήθης μετρική, δεν είναι φραγμένος.
![]() αυτό σημαίνει ότι για
αυτό σημαίνει ότι για
![]() και
και
![]() από τριγωνική ανισότητα έχουμε
από τριγωνική ανισότητα έχουμε
![]() για όλα
για όλα ![]() άρα ο
άρα ο
![]() φραγμένος.
φραγμένος.
![]()
![]() είναι ανοιχτό κάλυμμα του
είναι ανοιχτό κάλυμμα του ![]() . Αφού
. Αφού ![]() είναι συμπαγής
υπάρχουν
είναι συμπαγής
υπάρχουν
![]() ώστε
ώστε
![]() όπου
όπου
![]() . Άρα ο
. Άρα ο ![]() είναι φραγμένος.
είναι φραγμένος.
![]()
![]() είναι κλειστό του
είναι κλειστό του ![]() άρα
άρα ![]() είναι συμπαγής υπόχωρος του
συμπάγη χώρου
είναι συμπαγής υπόχωρος του
συμπάγη χώρου ![]() του μετρικού χώρου
του μετρικού χώρου
![]() , όπου
, όπου ![]() συνήθης μετρική.
συνήθης μετρική.
![]() ώστε
ώστε
![]()
![]() δεν είναι κλειστά στο
δεν είναι κλειστά στο ![]() άρα δεν είναι
συμπαγείς υπόχωροι (του
άρα δεν είναι
συμπαγείς υπόχωροι (του ![]() ). Παρατηρούμε ότι το δεύτερο σύνολο γίνεται συμπαγής αν προστεθεί το στοιχείο μηδέν.
). Παρατηρούμε ότι το δεύτερο σύνολο γίνεται συμπαγής αν προστεθεί το στοιχείο μηδέν.
![]() είναι συμπαγής. Τότε από το θεώρημα 1.5.2, είναι φραγμένος. Επίσης από
το θεώρημα 1.5.4, είναι και κλειστός.
είναι συμπαγής. Τότε από το θεώρημα 1.5.2, είναι φραγμένος. Επίσης από
το θεώρημα 1.5.4, είναι και κλειστός.
![]()
![]() , τα όποια θα τα χρησιμοποιούμε σε πολλά παραδείγματα στο κεφάλαιο 3. Όπως θα
δούμε αργότερα, τα σύνολα Cantor είναι σύνολα κλασματικής διάστασης.
, τα όποια θα τα χρησιμοποιούμε σε πολλά παραδείγματα στο κεφάλαιο 3. Όπως θα
δούμε αργότερα, τα σύνολα Cantor είναι σύνολα κλασματικής διάστασης.
![]() . Ορίζουμε
. Ορίζουμε ![]() και έστω
και έστω
![]() και
και
![]() . Συνεχίζουμε την διαδικασία διαλέγοντας υποδιαστήματα από κάθε διάστημα που
έχουμε ήδη φτιάξει. Για παράδειγμα, αν έχουμε ορίσει τα διαστήματα
. Συνεχίζουμε την διαδικασία διαλέγοντας υποδιαστήματα από κάθε διάστημα που
έχουμε ήδη φτιάξει. Για παράδειγμα, αν έχουμε ορίσει τα διαστήματα
![]() , τότε στο επόμενο βήμα ορίζουμε
, τότε στο επόμενο βήμα ορίζουμε
![]() ,
διαγράφοντας από την μέση κάθε διαστήματος
,
διαγράφοντας από την μέση κάθε διαστήματος ![]() ένα διάστημα μήκους
ένα διάστημα μήκους
![]() . Έτσι κάθε διάστημα
. Έτσι κάθε διάστημα ![]() που παράγεται έχει μήκος
που παράγεται έχει μήκος ![]() , βλέπε
σχήμα 1.1.
, βλέπε
σχήμα 1.1.
![]()
![]() είναι συμπαγές.
είναι συμπαγές.
![]() και
και ![]() . Είναι επίσης και κλειστό ως άπειρη τομή κλειστών συνόλων. Από
το θεώρημα 1.5.5 έπεται ότι το σύνολο Cantor είναι συμπαγές.
. Είναι επίσης και κλειστό ως άπειρη τομή κλειστών συνόλων. Από
το θεώρημα 1.5.5 έπεται ότι το σύνολο Cantor είναι συμπαγές.
![]()
![]() είναι συμπαγής.
είναι συμπαγής.
![]()
![]()
![]() είναι ακολουθιακά συμπαγής, υπάρχει μια υπακολουθία
είναι ακολουθιακά συμπαγής, υπάρχει μια υπακολουθία ![]() της
της ![]() η οποία συγκλίνει σε κάποιο
σημείο
η οποία συγκλίνει σε κάποιο
σημείο ![]() . Εφόσον η
. Εφόσον η ![]() είναι ανοιχτή κάλυψη, υπάρχει
είναι ανοιχτή κάλυψη, υπάρχει
![]() ώστε
ώστε
![]() . Αφού
. Αφού ![]() ανοιχτό, υπάρχει
ανοιχτό, υπάρχει ![]() ώστε
ώστε
![]() . Επιπλέον
. Επιπλέον
![]() είναι όριο της ακολουθίας
είναι όριο της ακολουθίας ![]() , άρα από κάποιο
, άρα από κάποιο ![]() και μετά όλα τα στοιχεία της
και μετά όλα τα στοιχεία της ![]() θα
βρίσκονται στην ανοιχτή μπάλα
θα
βρίσκονται στην ανοιχτή μπάλα
![]() , δηλαδή
, δηλαδή
![]() είναι ανοιχτό υποσύνολο του
είναι ανοιχτό υποσύνολο του ![]() και
και
![]() είναι ανοιχτή κάλυψη του
είναι ανοιχτή κάλυψη του ![]() , η οποία δεν έχει πεπερασμένη ανοιχτή υποκάλυψη, γιατι τα
, η οποία δεν έχει πεπερασμένη ανοιχτή υποκάλυψη, γιατι τα
![]() , άρα
ο
, άρα
ο ![]() δεν είναι συμπαγής, που είναι άτοπο, άρα
δεν είναι συμπαγής, που είναι άτοπο, άρα
![]() και ο
και ο ![]() έχει την ιδιότητα Bolzano - Weierstrass.
έχει την ιδιότητα Bolzano - Weierstrass.
![]() Έστω τώρα ότι ο
Έστω τώρα ότι ο ![]() έχει την ιδιότητα Bolzano - Weirstrass. Θεωρούμε την ακολουθία
έχει την ιδιότητα Bolzano - Weirstrass. Θεωρούμε την ακολουθία
![]() , θέλουμε να δείξουμε ότι η
, θέλουμε να δείξουμε ότι η ![]() έχει συγκλίνουσα υπακολουθία.
έχει συγκλίνουσα υπακολουθία.
![]() έχει πεπερασμένο το πλήθος στοιχείων, δηλαδή
έχει πεπερασμένο το πλήθος στοιχείων, δηλαδή
![]() . Θέτουμε
. Θέτουμε
![]() τότε
τότε
![]() . Τουλάχιστον ένα από τα
. Τουλάχιστον ένα από τα
![]() είναι
αριθμήσιμα άπειρο. Υποθέτουμε χωρίς βλάβη της γενικότητας ότι
είναι
αριθμήσιμα άπειρο. Υποθέτουμε χωρίς βλάβη της γενικότητας ότι ![]() έχει άπειρα στοιχεία
έχει άπειρα στοιχεία
![]() όπου
όπου
![]() . Για κάθε
. Για κάθε
![]() , άρα
, άρα
![]() . Οπότε υπάρχει
συγκλίνουσα υπακολουθία της
. Οπότε υπάρχει
συγκλίνουσα υπακολουθία της ![]() που έχει όριο στο
που έχει όριο στο ![]() .
.
![]() έχει αριθμήσιμο άπειρο το πλήθος στοιχείων, από τον ορισμό της ιδιότητας Bolzano -
Weierstrass, έχουμε ότι
έχει αριθμήσιμο άπειρο το πλήθος στοιχείων, από τον ορισμό της ιδιότητας Bolzano -
Weierstrass, έχουμε ότι
![]() . Άρα υπάρχει
. Άρα υπάρχει ![]() .
Κατασκευάζουμε στην συνέχεια την υπακολουθία μας
.
Κατασκευάζουμε στην συνέχεια την υπακολουθία μας
![]() Έστω τώρα
Έστω τώρα ![]() ακολουθιακά συμπαγής, θέλουμε να δείξουμε ότι είναι συμπαγής. Θεωρούμε ανοιχτή κάληψη
ακολουθιακά συμπαγής, θέλουμε να δείξουμε ότι είναι συμπαγής. Θεωρούμε ανοιχτή κάληψη
![]() του
του ![]() . Υποθέτουμε ότι η
. Υποθέτουμε ότι η ![]() δεν έχει πεπερασμένη υποκάλυψη (για να καταλήξουμε σε
άτοπο).
δεν έχει πεπερασμένη υποκάλυψη (για να καταλήξουμε σε
άτοπο).
![]() ώστε
ώστε
![]() να περιέχεται σε
κάποιο μέλος της
να περιέχεται σε
κάποιο μέλος της ![]() για κάθε
για κάθε ![]() . Οπότε υπάρχει
. Οπότε υπάρχει ![]() και
και
![]() με
με
![]() , υπάρχει επίσης
, υπάρχει επίσης
![]() και
και
![]() ώστε
ώστε
![]() . Τώρα έχουμε θεωρήσει πως
. Τώρα έχουμε θεωρήσει πως ![]() δεν έχει πεπερασμένη υπόκαλυψη,
άρα
δεν έχει πεπερασμένη υπόκαλυψη,
άρα
![]() . Άρα υπάρχει
. Άρα υπάρχει
![]() και
και
![]() με
με
![]() . Συνεχίζουμε έτσι και κατασκευάζουμε την ακολουθία
. Συνεχίζουμε έτσι και κατασκευάζουμε την ακολουθία
![]() , με
, με
![]() και να υπάρχει σύνολο
και να υπάρχει σύνολο
![]() ώστε
ώστε
![]() .
.
![]() ισχύει
ισχύει
![]() είναι ανοιχτή κάλυψη του συμπαγούς
είναι ανοιχτή κάλυψη του συμπαγούς
![]() . Από το θεώρημα 1.5.7 υπάρχει
. Από το θεώρημα 1.5.7 υπάρχει ![]() ώστε για κάθε
ώστε για κάθε ![]() η μπάλα
η μπάλα
![]() να περιέχεται σε κάποιο στοιχείο της
να περιέχεται σε κάποιο στοιχείο της ![]() . Έστω ότι
. Έστω ότι
![]() , τότε
, τότε
![]() για κάποιο
για κάποιο ![]() . Αφού
. Αφού
![]() και από τριγωνική ανισότητα
και από τριγωνική ανισότητα
![]() .
Άρα αν
.
Άρα αν
![]() .
.
![]() είναι ομοιόμορφα συνεχής.
είναι ομοιόμορφα συνεχής.
![]()
![]() είναι κλειστός και φραγμένος υπόχωρος του
είναι κλειστός και φραγμένος υπόχωρος του ![]() θέλουμε να δείξουμε ότι ο
θέλουμε να δείξουμε ότι ο ![]() είναι
συμπαγής. Αρκεί να δείξουμε ότι είναι ακολουθιακά συμπαγής. Θα το δείξουμε για
είναι
συμπαγής. Αρκεί να δείξουμε ότι είναι ακολουθιακά συμπαγής. Θα το δείξουμε για ![]() , δηλαδή
, δηλαδή
![]() , αφού η απόδειξη για οποιοδήποτε
, αφού η απόδειξη για οποιοδήποτε ![]() είναι παρόμοια (αλλά ίσως πιο πολύπλοκη).
είναι παρόμοια (αλλά ίσως πιο πολύπλοκη).
![]() του
του ![]() . Αφού ο
. Αφού ο ![]() είναι φραγμένος, υπάρχει κάποιο
είναι φραγμένος, υπάρχει κάποιο
![]() ώστε
ώστε ![]() για όλα τα
για όλα τα
![]() . Έτσι για κάθε
. Έτσι για κάθε
![]() έχουμε
έχουμε
![]() , οπότε
, οπότε ![]() είναι ακολουθίες στο συμπαγές
είναι ακολουθίες στο συμπαγές ![]() .
Άρα υπάρχει υπακολουθία
.
Άρα υπάρχει υπακολουθία ![]() της
της ![]() που να συγκλίνει σε σημείο
που να συγκλίνει σε σημείο ![]() του
του ![]() . Τώρα για το
ίδιο λόγο η ακολουθία
. Τώρα για το
ίδιο λόγο η ακολουθία ![]() έχει συγκλίνουσα υπακολουθία
έχει συγκλίνουσα υπακολουθία ![]() , όριο της οποίας είναι
, όριο της οποίας είναι ![]() .
.
![]() και
και
![]() , από το θεώρημα
1.3.3
, από το θεώρημα
1.3.3
![]() , έχουμε ότι η υπακολουθία
, έχουμε ότι η υπακολουθία
![]() της
της
![]() συγκλίνει σε σημείο του
συγκλίνει σε σημείο του ![]() , άρα ο
, άρα ο ![]() είναι ακολουθιακά συμπαγής.
είναι ακολουθιακά συμπαγής.
![]()