




Next: Αρχή της Συστολής
Up: Μετρική Τοπολογία
Previous: Συμπάγεια
Contents
Index
Απόδειξη: Έστω ότι η ακολουθία  συγκλίνει σε
συγκλίνει σε 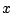 στο μετρικό χώρο
στο μετρικό χώρο  . Έστω
. Έστω  τότε
υπάρχει
τότε
υπάρχει
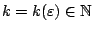 ώστε για κάθε
ώστε για κάθε 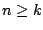 ισχύει
ισχύει
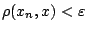 .
Τώρα για κάθε
.
Τώρα για κάθε 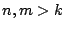 και από τριγωνική ανισότητα έχουμε
και από τριγωνική ανισότητα έχουμε
Άρα η  είναι ακολουθία Cauchy.
είναι ακολουθία Cauchy.

Δείξαμε προηγουμένως ότι κάθε συγκλίνουσα ακολουθία είναι ακολουθία Cauchy. Το αντίθετο
δεν ισχύει εν γένει, όταν ισχύει όμως έχουμε τον ορισμό του πλήρη χώρου.
Ορισμός 1.6.2
Έστω  μετρικός χώρος. Όταν κάθε ακολουθία Cauchy στο
μετρικός χώρος. Όταν κάθε ακολουθία Cauchy στο  συγκλίνει (σε σημείο
του
συγκλίνει (σε σημείο
του  ), τότε ο
), τότε ο  λέγεται πλήρης χώρος.
λέγεται πλήρης χώρος.
Παράδειγμα: Ο υπόχωρος 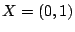 του
του  δεν είναι πλήρης αφού η ακολουθία
δεν είναι πλήρης αφού η ακολουθία
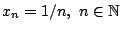 είναι στο
είναι στο  και είναι Cauchy αλλά δεν συγκλίνει στο
και είναι Cauchy αλλά δεν συγκλίνει στο  , (
, (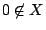 ).
).
Πρόταση 1.6.1
Μια ακολουθία Cauchy που έχει συγκλίνουσα υπακολουθία, συγκλίνει και η ίδια. Μάλιστα συγκλίνει στο
ίδιο σημείο που συγκλίνει η υπακολουθία.
Απόδειξη: Έστω  ακολουθία Cauchy μετρικού χώρου
ακολουθία Cauchy μετρικού χώρου  . Έστω
. Έστω 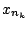 υπακολουθία με
υπακολουθία με
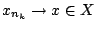 . Έστω
. Έστω  τότε από τον ορισμό της ακολουθίας Cauchy
υπάρχει
τότε από τον ορισμό της ακολουθίας Cauchy
υπάρχει
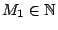 ώστε για κάθε
ώστε για κάθε 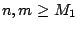 να ισχύει
να ισχύει
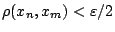 .
Τώρα επειδή
.
Τώρα επειδή
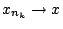 , υπάρχει
, υπάρχει
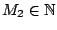 ώστε για κάθε
ώστε για κάθε 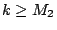 ισχύει
ισχύει
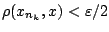 . Διαλέγουμε
. Διαλέγουμε
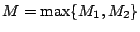 , τότε για κάθε
, τότε για κάθε 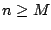 και
από την τριγωνική ανισότητα
και
από την τριγωνική ανισότητα

Απόδειξη: Έστω μια ακολουθία Cauchy  του μετρικού χώρου
του μετρικού χώρου  . Εφόσον ο
. Εφόσον ο  είναι συμπαγής, είναι και
ακολουθιακά συμπαγής, δηλαδή κάθε ακολουθία
είναι συμπαγής, είναι και
ακολουθιακά συμπαγής, δηλαδή κάθε ακολουθία  έχει συγκλίνουσα υπακολουθία
έχει συγκλίνουσα υπακολουθία 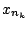 σε σημείο
του
σε σημείο
του  . Από την προηγούμενη πρόταση 1.6.1, βγάζουμε το συμπέρασμα ότι κάθε ακολουθία
Cauchy στο
. Από την προηγούμενη πρόταση 1.6.1, βγάζουμε το συμπέρασμα ότι κάθε ακολουθία
Cauchy στο  είναι συγκλίνουσα. Δηλαδή ο
είναι συγκλίνουσα. Δηλαδή ο  είναι πλήρης.
είναι πλήρης.

Παράδειγμα: Κάθε κλειστό και φραγμένο διάστημα ![$[a,b]$](images/img701.gif) του
του  είναι πλήρης υπόχωρος του
είναι πλήρης υπόχωρος του  .
.
Παράδειγμα: Ο 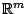 είναι πλήρης.
είναι πλήρης.
Απόδειξη: Έστω  είναι ακολουθία Cauchy στο
είναι ακολουθία Cauchy στο  . Από τον ορισμό της ακολουθίας Cauchy για
. Από τον ορισμό της ακολουθίας Cauchy για
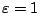 υπάρχει
υπάρχει
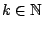 ώστε για κάθε
ώστε για κάθε 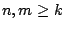 ισχύει ότι
ισχύει ότι
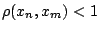 ,
δηλαδή από κάποιο
,
δηλαδή από κάποιο 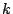 και μετά όλα τα στοιχεία της ακολουθίας
και μετά όλα τα στοιχεία της ακολουθίας  βρίσκονται σε μια μπάλα
βρίσκονται σε μια μπάλα 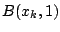 .
.
Έστω
 τότε όλη η ακολουθία
τότε όλη η ακολουθία  περιέχεται σε μπάλα
περιέχεται σε μπάλα
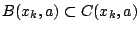 , όπου
, όπου 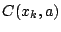 είναι μια κλειστή μπάλα. Η
είναι μια κλειστή μπάλα. Η 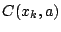 είναι συμπαγής υπόχωρος
του
είναι συμπαγής υπόχωρος
του 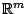 από το προηγούμενο θεώρημα 1.6.2 η
από το προηγούμενο θεώρημα 1.6.2 η 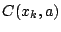 είναι πλήρης, άρα η
είναι πλήρης, άρα η
 συγκλίνει σε σημείο της
συγκλίνει σε σημείο της
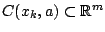 . Άρα ο
. Άρα ο 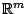 είναι πλήρης.
είναι πλήρης.

Η πληρότητα είναι μετρική ιδιότητα και αυτό
φαίνεται από την επόμενη πρόταση.
Πρόταση 1.6.2
Έστω  πλήρης μετρικός χώρος και
πλήρης μετρικός χώρος και  ένας κλειστός υπόχωρος του
ένας κλειστός υπόχωρος του  . Τότε ο
. Τότε ο  είναι πλήρης.
είναι πλήρης.
Απόδειξη: Έστω 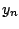 είναι μια ακολουθία Cauchy στο
είναι μια ακολουθία Cauchy στο  τότε
τότε 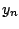 είναι ακολουθία Cauchy στο
πλήρη μετρικό χώρο
είναι ακολουθία Cauchy στο
πλήρη μετρικό χώρο  , δηλαδή
, δηλαδή
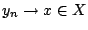 . Όμως
. Όμως
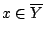 και
και
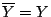 γιατί ο
γιατί ο  είναι κλειστός. Άρα ο
είναι κλειστός. Άρα ο  είναι πλήρης.
είναι πλήρης.

Πρόταση 1.6.3
Έστω  πλήρης υπόχωρος μετρικού χώρου
πλήρης υπόχωρος μετρικού χώρου  . Τότε
. Τότε  είναι κλειστός υπόχωρος του
είναι κλειστός υπόχωρος του  .
.
Απόδειξη: Αρκει να δείξουμε ότι
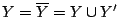 , δηλαδή
, δηλαδή 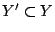 . Έστω
. Έστω 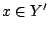 , τότε υπάρχει ακολουθία
, τότε υπάρχει ακολουθία 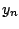 του
του  με
με
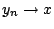 . Όμως ο
. Όμως ο  είναι πλήρης, άρα η
είναι πλήρης, άρα η 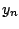 πρέπει να συγκλίνει σε σημείο του
πρέπει να συγκλίνει σε σημείο του  και αφού το όριο είναι μοναδικό,
και αφού το όριο είναι μοναδικό, 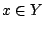 . Άρα ο
. Άρα ο  είναι κλειστός υπόχωρος του
είναι κλειστός υπόχωρος του  .
.

Πόρισμα 1.6.1
Αν
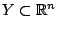 τότε
τότε  είναι πλήρης αν και μόνο αν το
είναι πλήρης αν και μόνο αν το  είναι κλειστό υποσύνολο του
είναι κλειστό υποσύνολο του
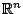 .
.
Subsections





Next: Αρχή της Συστολής
Up: Μετρική Τοπολογία
Previous: Συμπάγεια
Contents
Index
Khusainov Alexander
2002-10-25
![]() τότε όλη η ακολουθία
τότε όλη η ακολουθία ![]() περιέχεται σε μπάλα
περιέχεται σε μπάλα
![]() , όπου
, όπου ![]() είναι μια κλειστή μπάλα. Η
είναι μια κλειστή μπάλα. Η ![]() είναι συμπαγής υπόχωρος
του
είναι συμπαγής υπόχωρος
του ![]() από το προηγούμενο θεώρημα 1.6.2 η
από το προηγούμενο θεώρημα 1.6.2 η ![]() είναι πλήρης, άρα η
είναι πλήρης, άρα η
![]() συγκλίνει σε σημείο της
συγκλίνει σε σημείο της
![]() . Άρα ο
. Άρα ο ![]() είναι πλήρης.
είναι πλήρης.
![]()