




Next: Διαχωρίσιμοι Χώροι
Up: Πλήρεις και Διαχωρίσιμοι Χώροι
Previous: Πλήρεις και Διαχωρίσιμοι Χώροι
Contents
Index
Παράδειγμα: Η ομοιότητα ικανοποιεί την συνθήκη
Lipschitz.
Πρόταση 1.6.4
Έστω ότι η
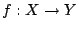 ικανοποιεί την σηνθήκη Lipschitz. Τότε η
ικανοποιεί την σηνθήκη Lipschitz. Τότε η  είναι ομοιόμορφα συνεχής.
είναι ομοιόμορφα συνεχής.
Απόδειξη: Αρκεί να πάρουμε για
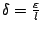

Πρόταση 1.6.5
Έστω
![$f:[a,b]\rightarrow [a,b]$](images/img726.gif) συνεχής και παραγωγίσιμη συνάρτηση με
συνεχής και παραγωγίσιμη συνάρτηση με 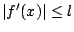 για κάθε
για κάθε 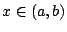 .
Τότε η
.
Τότε η  ικανοποιεί την συνθήκη Lipschitz. στο χώρο
ικανοποιεί την συνθήκη Lipschitz. στο χώρο ![$X=[a,b]$](images/img728.gif) με τη συνήθη μετρική
με τη συνήθη μετρική 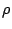 .
.
Απόδειξη: Έστω 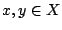 , υποθέτουμε ότι
, υποθέτουμε ότι 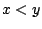 . Από το θεώρημα μέσης τιμής υπάρχει
. Από το θεώρημα μέσης τιμής υπάρχει 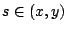 ώστε
ώστε
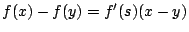 , αν πάρουμε σ'' αυτή τη σχέση την απόλυτη τιμή, έχουμε ότι
, αν πάρουμε σ'' αυτή τη σχέση την απόλυτη τιμή, έχουμε ότι
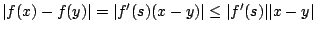 , όμως η συνήθης μετρική στο
, όμως η συνήθης μετρική στο  είναι η απόλυτη τιμή άρα
είναι η απόλυτη τιμή άρα
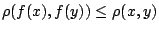 και η
και η  είναι συνάρτηση Lipschitz.
είναι συνάρτηση Lipschitz.

Πόρισμα 1.6.2
Αν
![$f:[a,b]\rightarrow [a,b]$](images/img726.gif) είναι συνεχής και παραγωγίσιμη συνάρτηση με
είναι συνεχής και παραγωγίσιμη συνάρτηση με 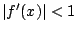 τότε η
τότε η  είναι συστολή.
είναι συστολή.
Θεώρημα 1.6.3
Αρχή της συστόλης (θεώρημα σταθερού σημείου Banach )
Έστω  είναι πλήρης μετρικός χώρος και η
είναι πλήρης μετρικός χώρος και η
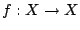 είναι μια συστολή. Τότε η
είναι μια συστολή. Τότε η  έχει μοναδικό
σταθερό σημείο
έχει μοναδικό
σταθερό σημείο 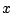 . Μάλιστα αν
. Μάλιστα αν 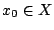 και το
και το
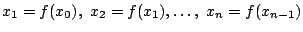 , τότε η
ακολουθία
, τότε η
ακολουθία  συγκλίνει σ'' αυτό το σημείο,
συγκλίνει σ'' αυτό το σημείο,
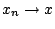 .
.
Απόδειξη: Παίρνουμε ένα τυχαίο σημείο 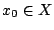 και ορίζουμε αναδρομικά την ακολουθία
και ορίζουμε αναδρομικά την ακολουθία  ως εξής
ως εξής
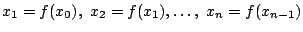 . Θα δείξουμε ότι η ακολουθία
. Θα δείξουμε ότι η ακολουθία  είναι Cauchy . Επειδή η
είναι Cauchy . Επειδή η  είναι συστολή, δηλαδή υπάρχει
είναι συστολή, δηλαδή υπάρχει 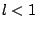 ώστε για κάθε
ώστε για κάθε 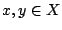 ισχύει
ισχύει
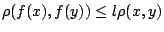 ,
έχουμε
,
έχουμε
Τώρα για κάθε
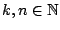 και από την τριγωνική ανισότητα
και από την τριγωνική ανισότητα
Όμως 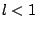 και
και
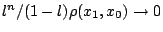 άρα υπάρχει
άρα υπάρχει
 και
και
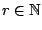 που να ισχύει ότι για κάθε
που να ισχύει ότι για κάθε 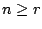
Τώρα για 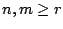 έχουμε ότι
έχουμε ότι
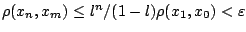 , άρα η ακολουθία
, άρα η ακολουθία
 είναι Cauchy και συγκλίνει σε κάποιο σημείο
είναι Cauchy και συγκλίνει σε κάποιο σημείο  , αφού ο
, αφού ο  είναι πλήρης.
Έχουμε δηλαδή ότι
είναι πλήρης.
Έχουμε δηλαδή ότι
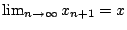 , άρα
, άρα
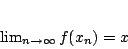 |
(1.13) |
Αφού
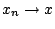 και η συνάρτηση
και η συνάρτηση  είναι συνεχής ως συστολή που είναι, έχουμε
είναι συνεχής ως συστολή που είναι, έχουμε
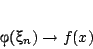 |
(1.14) |
Από τις σχέσεις 1.13 και 1.14
έχουμε ότι 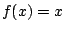 . Άρα
. Άρα 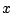 είναι σταθερό σημείο της
είναι σταθερό σημείο της  .
.
Τώρα έστω ότι έχουμε δύο σταθερά σημεία, δηλαδή 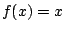 και
και 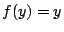 τότε
τότε
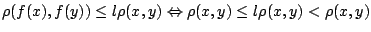 άτοπο αν
άτοπο αν
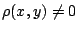 , άρα
, άρα 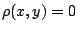 δηλαδή
δηλαδή 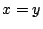 .
.






Next: Διαχωρίσιμοι Χώροι
Up: Πλήρεις και Διαχωρίσιμοι Χώροι
Previous: Πλήρεις και Διαχωρίσιμοι Χώροι
Contents
Index
Khusainov Alexander
2002-10-25
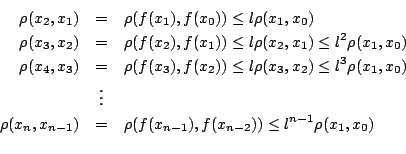
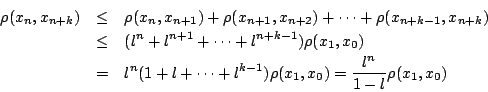
![]() και
και ![]() τότε
τότε
![]() άτοπο αν
άτοπο αν
![]() , άρα
, άρα ![]() δηλαδή
δηλαδή ![]() .
.
![]()