




Next: Ομοιόμορφη Σύγκλιση Συναρτήσεων
Up: Πλήρεις και Διαχωρίσιμοι Χώροι
Previous: Αρχή της Συστολής
Contents
Index
Ορισμός 1.6.5
Ένας μετρικός χώρος  λέγεται
διαχωρίσιμος αν υπάρχει αριθμήσιμο
υποσύνολο
λέγεται
διαχωρίσιμος αν υπάρχει αριθμήσιμο
υποσύνολο  του
του  ώστε το
ώστε το  να είναι πυκνό, δηλαδή
να είναι πυκνό, δηλαδή
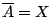 .
.
Παράδειγμα: Ο μετρικός χώρος
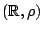 , όπου
, όπου 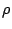 είναι η συνήθης μετρική στο
είναι η συνήθης μετρική στο  , είναι
διαχωρίσιμος, γιατί το σύνολο των ρητών αριθμών
, είναι
διαχωρίσιμος, γιατί το σύνολο των ρητών αριθμών 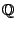 είναι αριθμήσιμο και πυκνό υποσύνολο του
είναι αριθμήσιμο και πυκνό υποσύνολο του
 .
.
Παράδειγμα: Ο μετρικός χώρος
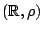 , όπου
, όπου 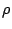 είναι η διακριτή μετρική, δεν είναι διαχωρίσιμος. Αφού
έχουμε ότι για κάθε
είναι η διακριτή μετρική, δεν είναι διαχωρίσιμος. Αφού
έχουμε ότι για κάθε
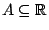 ισχύει
ισχύει
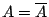 , άρα το μόνο πυκνό υποσύνολο του
, άρα το μόνο πυκνό υποσύνολο του
 είναι ο εαυτός του, που όμως δεν είναι αριθμήσιμο.
είναι ο εαυτός του, που όμως δεν είναι αριθμήσιμο.
Παράδειγμα: Ο μετρικός χώρος
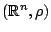 , όπου
, όπου 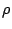 είναι η συνήθης μετρική στο
είναι η συνήθης μετρική στο 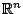 , είναι
διαχωρίσιμος, γιατί
, είναι
διαχωρίσιμος, γιατί 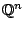 είναι αριθμήσιμο και πυκνό υποσύνολο του
είναι αριθμήσιμο και πυκνό υποσύνολο του 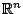 .
.
Απόδειξη: Έστω ένα μη κενό ανοιχτό υποσύνολο 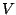 του
του 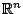 , τότε υπάρχει
, τότε υπάρχει
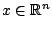 και
και
 με
με
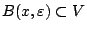 . Τώρα αν
. Τώρα αν
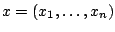 τότε υπάρχουν
τότε υπάρχουν
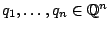 ώστε
ώστε
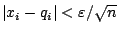 για
για
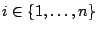 .
Τότε το
.
Τότε το
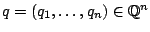 και
και
άρα
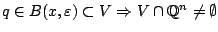 , δηλαδή
, δηλαδή
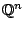 πυκνό υποσύνολο του
πυκνό υποσύνολο του 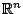 .
.

Θεώρημα 1.6.4
Έστω  είναι ένας μετρικός χώρος. Τότε ο
είναι ένας μετρικός χώρος. Τότε ο  είναι διαχωρίσιμος αν και μόνο αν κάθε ανοιχτή
κάλυψη του
είναι διαχωρίσιμος αν και μόνο αν κάθε ανοιχτή
κάλυψη του  έχει αριθμήσιμη υποκάλυψη.
έχει αριθμήσιμη υποκάλυψη.
Απόδειξη: Υποθέτουμε πρώτα ότι ο  είναι διαχωρίσιμος, θέλουμε να δείξουμε ότι κάθε ανοιχτή κάλυψη του
είναι διαχωρίσιμος, θέλουμε να δείξουμε ότι κάθε ανοιχτή κάλυψη του  έχει αριθμήσιμη
υποκάλυψη. Αφού ο
έχει αριθμήσιμη
υποκάλυψη. Αφού ο  είναι διαχωρίσιμος υπάρχει
είναι διαχωρίσιμος υπάρχει
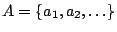 πυκνό υποσύνολο του
πυκνό υποσύνολο του  ,
δηλαδή
,
δηλαδή
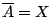 . Θεωρούμε μια ανοιχτή κάλυψη
. Θεωρούμε μια ανοιχτή κάλυψη  του
του  . Συμβολίζουμε
. Συμβολίζουμε
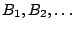 τις αριθμήσιμες ανοιχτές μπάλες
τις αριθμήσιμες ανοιχτές μπάλες 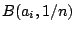 , όπου
, όπου
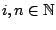 , που περιέχονται
σε κάποιο μέλος της
, που περιέχονται
σε κάποιο μέλος της  . Συμβολίζουμε επίσης,
. Συμβολίζουμε επίσης,
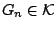 για κάθε
για κάθε
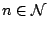 ,
ώστε το
,
ώστε το 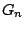 να περιέχει την αντίστοιχη ανοιχτή μπάλα
να περιέχει την αντίστοιχη ανοιχτή μπάλα 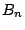 . Αρκεί να δείξουμε ότι
. Αρκεί να δείξουμε ότι
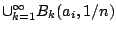 , οπότε η υποκάλυψη
, οπότε η υποκάλυψη
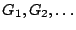 της
της  θα είναι
αριθμήσιμη. Έστω
θα είναι
αριθμήσιμη. Έστω  . Αρκεί να βρούμε
. Αρκεί να βρούμε
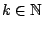 με
με
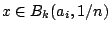 για κάποια
για κάποια
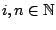 . Πρέπει να υπάρχει ανοιχτό σύνολο
. Πρέπει να υπάρχει ανοιχτό σύνολο
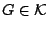 με
με 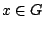 , αφού
, αφού  είναι κάλυψη το
είναι κάλυψη το  . Άρα υπάρχει
. Άρα υπάρχει
 ώστε
ώστε
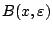 . Έστω
. Έστω
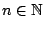 με
με
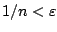 θα υπάρχει
θα υπάρχει
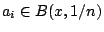 , αφού
, αφού
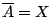 , δηλαδή
, δηλαδή
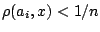 , που
σημαίνει ότι
, που
σημαίνει ότι
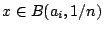 . Θέτουμε
. Θέτουμε
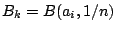 για κάποιο
για κάποιο
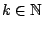 τότε
τότε 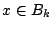 , άρα
, άρα
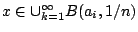 , δηλαδή
, δηλαδή
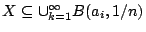 (ότι
(ότι
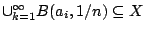 είναι φανερό).
είναι φανερό).
Αντίστροφα, έστω ότι κάθε ανοιχτή κάλυψη του  έχει αριθμήσιμη υποκάλυψη, τότε θέλουμε να δείξουμε ότι ο
έχει αριθμήσιμη υποκάλυψη, τότε θέλουμε να δείξουμε ότι ο  είναι διαχωρίσιμος, δηλαδή ότι υπάρχει πυκνό και αριθμήσιμο υποσύνολο
είναι διαχωρίσιμος, δηλαδή ότι υπάρχει πυκνό και αριθμήσιμο υποσύνολο  του
του  . Έστω η ανοιχτή κάλυψη
. Έστω η ανοιχτή κάλυψη
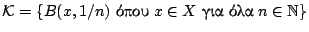 του
του  . Από την
υπόθεση υπάρχει αριθμήσιμη υποκάλυψη
. Από την
υπόθεση υπάρχει αριθμήσιμη υποκάλυψη
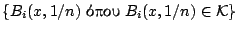 .
Θεωρούμε ότι
.
Θεωρούμε ότι
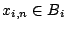 τότε η υποκάλυψη γράφεται
τότε η υποκάλυψη γράφεται
 |
(1.15) |
Το
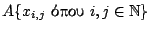 είναι αριθμήσιμο σύνολο. Έστω ένα μη κενό ανοιχτό
υποσύνολο
είναι αριθμήσιμο σύνολο. Έστω ένα μη κενό ανοιχτό
υποσύνολο 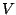 του
του  , τότε υπάρχει
, τότε υπάρχει
 και
και  ώστε
ώστε
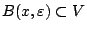 .
Έστω
.
Έστω
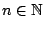 με
με
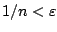 . Η σχέση 1.15 λέει
ότι υπάρχουν
. Η σχέση 1.15 λέει
ότι υπάρχουν
 τέτοια ώστε
τέτοια ώστε
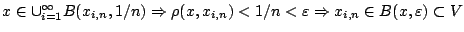 ,
,
Άρα
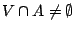 δηλαδή
δηλαδή  είναι πυκνό υποσύνολο του
είναι πυκνό υποσύνολο του  . Άρα ο
. Άρα ο  είναι διαχωρίσιμος.
είναι διαχωρίσιμος.

Khusainov Alexander
2002-10-25
![]() έχει αριθμήσιμη υποκάλυψη, τότε θέλουμε να δείξουμε ότι ο
έχει αριθμήσιμη υποκάλυψη, τότε θέλουμε να δείξουμε ότι ο ![]() είναι διαχωρίσιμος, δηλαδή ότι υπάρχει πυκνό και αριθμήσιμο υποσύνολο
είναι διαχωρίσιμος, δηλαδή ότι υπάρχει πυκνό και αριθμήσιμο υποσύνολο ![]() του
του ![]() . Έστω η ανοιχτή κάλυψη
. Έστω η ανοιχτή κάλυψη
![]() του
του ![]() . Από την
υπόθεση υπάρχει αριθμήσιμη υποκάλυψη
. Από την
υπόθεση υπάρχει αριθμήσιμη υποκάλυψη
![]() .
Θεωρούμε ότι
.
Θεωρούμε ότι
![]() τότε η υποκάλυψη γράφεται
τότε η υποκάλυψη γράφεται
![]() δηλαδή
δηλαδή ![]() είναι πυκνό υποσύνολο του
είναι πυκνό υποσύνολο του ![]() . Άρα ο
. Άρα ο ![]() είναι διαχωρίσιμος.
είναι διαχωρίσιμος.
![]()