




Next: Συστήματα Αρίθμησης
Up: Μετρική Τοπολογία
Previous: Διαχωρίσιμοι Χώροι
Contents
Index
Θεώρημα 1.7.1
Έστω η συνάρτηση
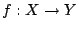 και η ακολουθία συναρτήσεων
και η ακολουθία συναρτήσεων
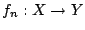 από το μετρικό
χώρο
από το μετρικό
χώρο  στο μετρικό χώρο
στο μετρικό χώρο 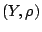 . Έστω ότι η ακολουθία
. Έστω ότι η ακολουθία 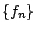 συγκλίνει ομοιόμορφα στη
συγκλίνει ομοιόμορφα στη
 και για όλα τα
και για όλα τα
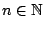 και οι συναρτήσεις
και οι συναρτήσεις 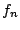 είναι συνεχείς. Τότε η
είναι συνεχείς. Τότε η  είναι συνεχής
συνάρτηση.
είναι συνεχής
συνάρτηση.
Απόδειξη: Έστω  . Πρέπει να δείξουμε ότι η συνάρτηση
. Πρέπει να δείξουμε ότι η συνάρτηση  είναι συνεχής στο
είναι συνεχής στο 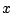 . Έστω
. Έστω
 πρέπει να βρούμε
κατάλληλο
πρέπει να βρούμε
κατάλληλο 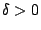 ώστε για κάθε
ώστε για κάθε 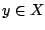 που ικανοποιεί
που ικανοποιεί
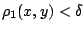 να ισχύει ότι
να ισχύει ότι
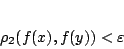 |
(1.16) |
Έτσι λοιπόν, από την τριγωνική ανισότητα και για όλα τα
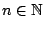 έχουμε ότι για κάθε
έχουμε ότι για κάθε 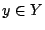 ισχύει
ισχύει
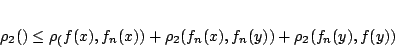 |
(1.17) |
Επειδή η ακολουθία συναρτήσεων 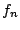 συγκλίνει ομοιόμορφα στην
συγκλίνει ομοιόμορφα στην  , υπάρχει
, υπάρχει
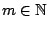 τέτοιο
ώστε για κάθε
τέτοιο
ώστε για κάθε 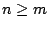 ισχύει ότι
ισχύει ότι
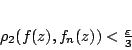 |
(1.18) |
για κάθε 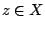
Διαλέγουμε 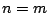 , τότε και αφού η
, τότε και αφού η 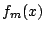 είναι συνεχής συνάρτηση, υπάρχει
είναι συνεχής συνάρτηση, υπάρχει
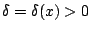 τέτοιο
ώστε
τέτοιο
ώστε
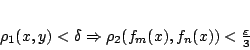 |
(1.19) |
Από τις προτάσεις 1.17,1.18
και 1.19 ισχύει η πρόταση 1.16.
Άρα η  είναι συνεχής συνάρτηση.
είναι συνεχής συνάρτηση.

Ορισμός 1.7.2
Μια συνάρτηση
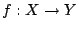 από μετρικό χώρο
από μετρικό χώρο 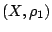 στο μετρικό χώρο
στο μετρικό χώρο 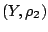 λέγεται
φραγμένη αν η εικόνα
λέγεται
φραγμένη αν η εικόνα ![$f[X]$](images/img430.gif) είναι
φραγμένο υποσύνολο του
είναι
φραγμένο υποσύνολο του  , δηλαδή αν και μόνο αν το σύνολο
, δηλαδή αν και μόνο αν το σύνολο
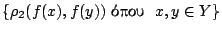 είναι φραγμένο υποσύνολο του
είναι φραγμένο υποσύνολο του  .
.
Έστω μετρικοί χώροι 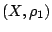 και
και 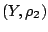 . Οριζούμε το σύνολο όλων των συνεχών συναρτήσεων
από το μετρικό χώρο
. Οριζούμε το σύνολο όλων των συνεχών συναρτήσεων
από το μετρικό χώρο  στο μετρικό χώρο
στο μετρικό χώρο  να είναι
να είναι
Πρόταση 1.7.1
Έστω ότι για όλα τα
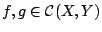 έχουμε
Τότε η
έχουμε
Τότε η 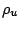 είναι μετρική στο
είναι μετρική στο
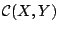 .
.
Απόδειξη: Είναι προφανές ότι η 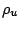 είναι θετική και αν
είναι θετική και αν 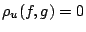 τότε
τότε 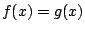 . Επίσης
. Επίσης
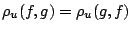 .
.
Τώρα σχετικά με την τριγωνική ανισότητα έχουμε ότι για κάθε  ισχύει
ισχύει
Άρα η 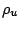 είναι μετρική.
είναι μετρική.

Η 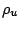 λέγεται η συνήθης μετρική στο μετρικό χώρο
λέγεται η συνήθης μετρική στο μετρικό χώρο
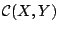 .
.
Θεώρημα 1.7.2
Έστω 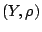 είναι ένας πλήρης μετρικός χώρος, τότε και ο
είναι ένας πλήρης μετρικός χώρος, τότε και ο
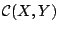 είναι πλήρης.
είναι πλήρης.
Απόδειξη: Έτσω 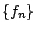 ακολουθία Cauchy στο μετρικό χώρο
ακολουθία Cauchy στο μετρικό χώρο
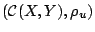 , δηλαδή για κάθε
, δηλαδή για κάθε
 , υπάρχει
, υπάρχει
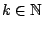 ώστε
ώστε
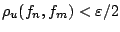 για κάθε
για κάθε 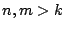 . Δηλαδή
για κάθε
. Δηλαδή
για κάθε 
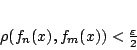 |
(1.20) |
άρα η 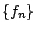 είναι ακολουθία Cauchy στο μετρικό χώρο
είναι ακολουθία Cauchy στο μετρικό χώρο 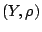 . Όμως ο
. Όμως ο  είναι πλήρης άρα
είναι πλήρης άρα
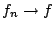 του
του  , δηλαδή υπάρχει
, δηλαδή υπάρχει 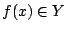 ώστε για κάθε
ώστε για κάθε  η
η
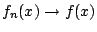 .
Τώρα γι'' αυτήν την συνάρτηση
.
Τώρα γι'' αυτήν την συνάρτηση
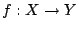 έχουμε, από την τριγωνική ανισότητα, ότι για κάθε
έχουμε, από την τριγωνική ανισότητα, ότι για κάθε  και για κάθε
και για κάθε
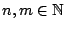
 |
(1.21) |
Τώρα δεδομένο ότι  και
και
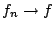 , υπάρχει
, υπάρχει
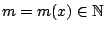 ώστε
ώστε
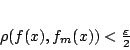 |
(1.22) |
Από τις προτάσεις 1.21,1.20
και 1.22, έχουμε ότι για κάθε 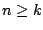 και για κάθε
και για κάθε  ισχύει
ισχύει
άρα η 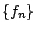 συγκλίνει ομοιόμορφα στην
συγκλίνει ομοιόμορφα στην  . Από το θεώρημα 1.7.1 η
. Από το θεώρημα 1.7.1 η  είναι συνεχής άρα ανήκει στο
είναι συνεχής άρα ανήκει στο
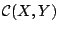 οπότε ο
οπότε ο
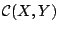 είναι πλήρης.
είναι πλήρης.

Πιο απλά η συσχετιζόμενη συνάρτηση είναι συνδυιασμός γραμμικού μετασχηματισμού και παραλλήλης μεταφοράς.
Πρόταση 1.7.2
Μια συσχετιζόμενη συνάρτηση
![$f:[a,b]\rightarrow \mathbb{R}$](images/img832.gif) πρέπει να είναι της μορφής
πρέπει να είναι της μορφής
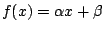 όπου
όπου
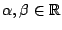
Απόδειξη: Αν 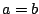 τότε δεν έχει νόημα να συζητάμε, οπότε υποθέτουμε ότι
τότε δεν έχει νόημα να συζητάμε, οπότε υποθέτουμε ότι 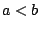 . Τώρα αν
. Τώρα αν ![$x\in [a,b]$](images/img836.gif) τότε
τότε
που είναι της μορφής 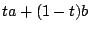 ,
, ![$t\in [0,1]$](images/img444.gif) . Άρα
. Άρα
αν
έχουμε το ζητούμενο.

Μια συνεχής καμπύλη στο μετρικό χώρο  είναι η εικόνα
μιάς συνεχής συνάρτησης
είναι η εικόνα
μιάς συνεχής συνάρτησης
![$f:[0,1]\rightarrow X$](images/img841.gif) .
.
Ορισμός 1.7.4
Μια συνεχής καμπύλη ![$f[0,1]$](images/img842.gif) στον
στον 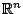 , όπου
, όπου 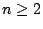 λέγεται γεμίζουσα τον χώρο καμπύλη αν και μόνο αν η
λέγεται γεμίζουσα τον χώρο καμπύλη αν και μόνο αν η ![$f[0,1]$](images/img842.gif) περιέχει μια ανοιχτή μπάλα με κέντρο
περιέχει μια ανοιχτή μπάλα με κέντρο 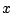 και ακτίνα
και ακτίνα 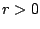 , όπου
, όπου
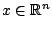 .
.





Next: Συστήματα Αρίθμησης
Up: Μετρική Τοπολογία
Previous: Διαχωρίσιμοι Χώροι
Contents
Index
Khusainov Alexander
2002-10-25
![]() , τότε και αφού η
, τότε και αφού η ![]() είναι συνεχής συνάρτηση, υπάρχει
είναι συνεχής συνάρτηση, υπάρχει
![]() τέτοιο
ώστε
τέτοιο
ώστε
![]() είναι συνεχής συνάρτηση.
είναι συνεχής συνάρτηση.
![]()
![]() και
και ![]() . Οριζούμε το σύνολο όλων των συνεχών συναρτήσεων
από το μετρικό χώρο
. Οριζούμε το σύνολο όλων των συνεχών συναρτήσεων
από το μετρικό χώρο ![]() στο μετρικό χώρο
στο μετρικό χώρο ![]() να είναι
να είναι
![]() ισχύει
ισχύει
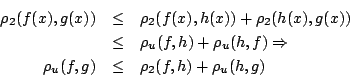
![]() λέγεται η συνήθης μετρική στο μετρικό χώρο
λέγεται η συνήθης μετρική στο μετρικό χώρο
![]() .
.
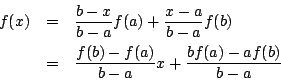
![]() είναι η εικόνα
μιάς συνεχής συνάρτησης
είναι η εικόνα
μιάς συνεχής συνάρτησης
![]() .
.