




Next: Μετρική Hausdorff
Up: Μετρική Τοπολογία
Previous: Ομοιόμορφη Σύγκλιση Συναρτήσεων
Contents
Index
Ας δούμε το συνηθισμένο δεκαδικό σύστημα αναπαράστασης των πραγματικών αριθμών και πως αυτό
μπορεί να γενικευτεί. Έστω ότι έχουμε έναν αριθμό 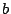 που θα είναι η βάση του συστήματός μας και
ένα πεπερασμένο σύνολο
που θα είναι η βάση του συστήματός μας και
ένα πεπερασμένο σύνολο
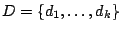 που είναι τα ψηφία μας. Υποθέτουμε ότι το
που είναι τα ψηφία μας. Υποθέτουμε ότι το 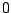 είναι ένα
από τα ψηφία. Ένας ακέραιος αριθμός, για όλα τα συστήματα, θα έχει την μορφή
είναι ένα
από τα ψηφία. Ένας ακέραιος αριθμός, για όλα τα συστήματα, θα έχει την μορφή
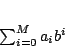 |
(1.23) |
όπου 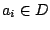 είναι ένα από τα ψηφία. Μη ακέραιος θα έχει την μορφή
είναι ένα από τα ψηφία. Μη ακέραιος θα έχει την μορφή
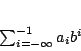 |
(1.24) |
όπου 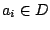 είναι κάποιο από τα ψηφία. Η γενική αναπαράσταση του αριθμού θα έχει την μορφή
είναι κάποιο από τα ψηφία. Η γενική αναπαράσταση του αριθμού θα έχει την μορφή
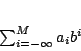 |
(1.25) |
Για να συγκλίνουν οι αναπαραστάσεις 1.24 και 1.25
θα πρέπει να μπεί ο περιορισμός 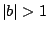
Το συνηθισμένο δεκαδικό μας σύστημα έχει
Το δυαδικό συστημά αρίθμησης, που τόσο πολύ χρησιμοποιείται στην επιστήμη των Η/Υ, έχει
Σ'' αυτές τις δύο περιπτώσεις ο τύπος 1.25 μπορεί να αναπαραστήσει όλους
τους αριθμούς που ανήκουν στο 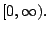
Και στις δύο περιπτώσεις οι αρνητικοί αριθμοί δεν μπορούν να αναπαρασταθούν, για να λύσουμε το πρόβλημα
απλά πολλαπλασιάζουμε τις σχέσεις 1.23, 1.24 και
1.25 με το 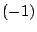 .
.
Το δεκαδικό και το δυαδικό σύστημα έχουν την ιδιομορφία ότι μερικοί αριθμοί έχουν δύο διαφορετικές
αναπαραστάσεις, για παράδειγμα
Θα εξετάσουμε το τριαδικό σύστημα αρίθμησης. Στο τριαδικό συστήμα έχουμε
Για παράδειγμα
θα γράφουμε ότι 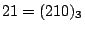 όπου ο δείκτης μας λέει πια είναι η βάση του συστήματος (εννοείται ότι
στο δεκαδικό σύστημα το παραλείπουμε) και η θέση του ψηφίου δείχνει σε πια δύναμη θα είναι υψώμενη η
βάση την οποία και θα πολλαπλασιάσει. Η θέση το ψηφίου μετριέται θετικά προς τα αριστερά από τo
κόμμα και αρνητικά προς τα δεξιά.
όπου ο δείκτης μας λέει πια είναι η βάση του συστήματος (εννοείται ότι
στο δεκαδικό σύστημα το παραλείπουμε) και η θέση του ψηφίου δείχνει σε πια δύναμη θα είναι υψώμενη η
βάση την οποία και θα πολλαπλασιάσει. Η θέση το ψηφίου μετριέται θετικά προς τα αριστερά από τo
κόμμα και αρνητικά προς τα δεξιά.
Παράδειγμα:
Μερικοί αριθμοί στο τριαδικό σύστημα και ειδικά οι αριθμοί τις μορφής  έχουν δύο διαφορετικές
αναπαραστάσεις, για παράδειγμα
έχουν δύο διαφορετικές
αναπαραστάσεις, για παράδειγμα
Figure:
Το τριαδικό σύνολο Cantor και τα πρώτα βήματα κατασκευής του
|
Πρόταση 1.8.1
Έστω ![$x\in [0,1]$](images/img861.gif) . Τότε το
. Τότε το
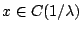 (τριαδικό σύνολο Cantor ) αν και μόνο αν η
αναπαράσταση του
(τριαδικό σύνολο Cantor ) αν και μόνο αν η
αναπαράσταση του 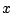 στο τριαδικό σύστημα αρίθμησης μπορεί να χρησιμοποιήσει μόνο τα ψηφία
στο τριαδικό σύστημα αρίθμησης μπορεί να χρησιμοποιήσει μόνο τα ψηφία 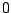 και
και 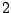 .
.
Απόδειξη: Στην πρώτη θέση από δεξία (μετά το κόμμα) στην τριαδική αναπαράσταση είναι 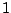 αν και μόνο αν το
αν και μόνο αν το 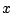 είναι ανάμεσα από
είναι ανάμεσα από
Τώρα το
![$C_1(1/\lambda )=[0,1/3]\cup[2/3,1]$](images/img865.gif) οπότε, αφού
οπότε, αφού
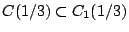 , το πρώτο ψηφίο μετά το
κόμμα για τα σημεία που ανήκουν στο σύνολο
, το πρώτο ψηφίο μετά το
κόμμα για τα σημεία που ανήκουν στο σύνολο 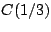 δεν είναι
δεν είναι 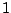 ( τα σημεία
( τα σημεία 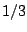 και
και 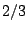 έχουν δύο
αναπαραστάσεις,
έχουν δύο
αναπαραστάσεις,
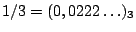 και
και 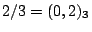 ). Η δεύτερη θέση σε τριαδική αναπαράσταση
του σημείου του συνόλου
). Η δεύτερη θέση σε τριαδική αναπαράσταση
του σημείου του συνόλου 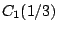 είναι
είναι 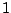 αν και μόνο αν ανήκει στα διαστήματα
αν και μόνο αν ανήκει στα διαστήματα 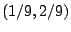 ή
ή 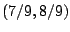 .
Τώρα
.
Τώρα
οπότε τα σημεία του 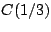 δεν περιέχουν
δεν περιέχουν 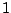 ούτε στην δεύτερη θέση μετά το κόμμα. Συνεχίζοτας
έτσι δείχνουμε ότι ένα σημείο που ανήκει στο
ούτε στην δεύτερη θέση μετά το κόμμα. Συνεχίζοτας
έτσι δείχνουμε ότι ένα σημείο που ανήκει στο 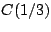 μπορεί να αναπαρασταθεί στην τριαδική μορφή
χρησιμοποιώντας μόνο τα ψηφία
μπορεί να αναπαρασταθεί στην τριαδική μορφή
χρησιμοποιώντας μόνο τα ψηφία 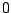
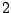 και καθόλου
και καθόλου 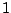 .
.

Πρόταση 1.8.2
Το τριαδικό σύνολο Cantor , 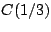 , είναι υπεραριθμήσιμο.
, είναι υπεραριθμήσιμο.
Απόδειξη: Τα στοιχεία του ![$[0,1]$](images/img875.gif) στην δυαδική αναπαράσταση είναι της μορφής
στην δυαδική αναπαράσταση είναι της μορφής
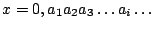 όπου
όπου 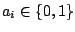 . Ορίζουμε το σύνολο
. Ορίζουμε το σύνολο  να περέχει όλα τα σημεία του
να περέχει όλα τα σημεία του ![$[0,1]$](images/img875.gif) σε δυαδικη μορφή και
σύνολο
σε δυαδικη μορφή και
σύνολο 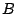 όλα τα σημεία του συνόλου Cantor ,
όλα τα σημεία του συνόλου Cantor , 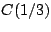 σε τριαδική μορφή, αλλά χωρίς να
χρησιμοποιείται το ψηφίο
σε τριαδική μορφή, αλλά χωρίς να
χρησιμοποιείται το ψηφίο 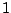 (από την προηγούμενη πρόταση μπορούμε να το κάνουμε). Δηλαδή αν
(από την προηγούμενη πρόταση μπορούμε να το κάνουμε). Δηλαδή αν 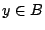 τότε το
τότε το
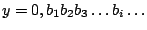 όπου
όπου
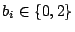 .
.
Ορίζουμε ένα προς ένα και επί την συνάρτηση από το  στο
στο 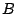 , που στέλνει το
, που στέλνει το 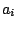 στο
στο 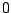 αν
αν 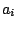 είναι
είναι 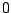 και στο
και στο 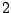 αν το
αν το 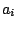 είναι
είναι 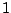 .
.
Άρα το σύνολο 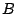 έχει το ίδιο πληθικό αριθμό στοιχείων με το
έχει το ίδιο πληθικό αριθμό στοιχείων με το  , δηλαδή το
, δηλαδή το ![$[0,1]$](images/img875.gif) . Όμως το
. Όμως το ![$[0,1]$](images/img875.gif) είναι
υπεραριθμήσιμο. Άρα το σύνολο
είναι
υπεραριθμήσιμο. Άρα το σύνολο 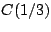 είναι υπεραριθμήσιμο.
είναι υπεραριθμήσιμο.






Next: Μετρική Hausdorff
Up: Μετρική Τοπολογία
Previous: Ομοιόμορφη Σύγκλιση Συναρτήσεων
Contents
Index
Khusainov Alexander
2002-10-25
![]() που θα είναι η βάση του συστήματός μας και
ένα πεπερασμένο σύνολο
που θα είναι η βάση του συστήματός μας και
ένα πεπερασμένο σύνολο
![]() που είναι τα ψηφία μας. Υποθέτουμε ότι το
που είναι τα ψηφία μας. Υποθέτουμε ότι το ![]() είναι ένα
από τα ψηφία. Ένας ακέραιος αριθμός, για όλα τα συστήματα, θα έχει την μορφή
είναι ένα
από τα ψηφία. Ένας ακέραιος αριθμός, για όλα τα συστήματα, θα έχει την μορφή
![]() .
.
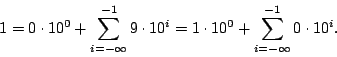
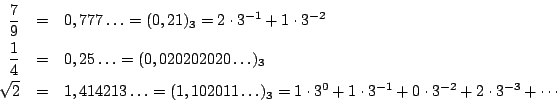
![]() έχουν δύο διαφορετικές
αναπαραστάσεις, για παράδειγμα
έχουν δύο διαφορετικές
αναπαραστάσεις, για παράδειγμα
![]() στο
στο ![]() , που στέλνει το
, που στέλνει το ![]() στο
στο ![]() αν
αν ![]() είναι
είναι ![]() και στο
και στο ![]() αν το
αν το ![]() είναι
είναι ![]() .
.
![]() έχει το ίδιο πληθικό αριθμό στοιχείων με το
έχει το ίδιο πληθικό αριθμό στοιχείων με το ![]() , δηλαδή το
, δηλαδή το ![]() . Όμως το
. Όμως το ![]() είναι
υπεραριθμήσιμο. Άρα το σύνολο
είναι
υπεραριθμήσιμο. Άρα το σύνολο ![]() είναι υπεραριθμήσιμο.
είναι υπεραριθμήσιμο.
![]()