




Next: Συνέχεια Συναρτήσεων
Up: Μετρικοί Χώροι
Previous: Μετρικοί Χώροι
Contents
Index
Ορισμός 1.1.2
Έστω  μετρικός χώρος. Μια ανοιχτή μπάλα με ακτίνα
μετρικός χώρος. Μια ανοιχτή μπάλα με ακτίνα 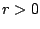 και
κέντρο το στοιχείο
και
κέντρο το στοιχείο 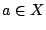 είναι το σύνολο
είναι το σύνολο
Ορισμός 1.1.3
Έστω  μετρικός χώρος. Μια κλειστή μπάλα με ακτίνα
μετρικός χώρος. Μια κλειστή μπάλα με ακτίνα 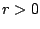 και
κέντρο το στοιχείο
και
κέντρο το στοιχείο 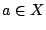 είναι το σύνολο
είναι το σύνολο
Προφανώς
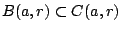 . Μερικά παραδείγματα:
. Μερικά παραδείγματα:
Παράδειγμα: Στο  , με την συνήθη μετρική, η ανοιχτή μπάλα εμφανίζεται σαν ανοιχτό διάστημα (δηλαδή
διάστημα της μορφής
, με την συνήθη μετρική, η ανοιχτή μπάλα εμφανίζεται σαν ανοιχτό διάστημα (δηλαδή
διάστημα της μορφής 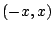 ).
).
Ενώ η κλειστή μπάλα εμφανίζεται σαν κλειστό διάστημα.
Παράδειγμα: Στο 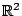 με την συνήθη μετρική η ανοιχτή μπάλα είναι ο ανοιχτός δίσκος με κέντρο
με την συνήθη μετρική η ανοιχτή μπάλα είναι ο ανοιχτός δίσκος με κέντρο 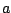 και
ακτίνα
και
ακτίνα 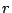 (δηλαδή ο δίσκος χωρίς τον κύκλο
(δηλαδή ο δίσκος χωρίς τον κύκλο
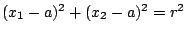 ).
).
Ενώ η κλειστή μπάλα εμφανίζεται σαν τον δίσκο ακτίνας 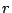 και με κέντρο
και με κέντρο 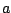 .
.
Παράδειγμα: Στο 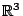 με την συνήθη μετρική η ανοιχτή μπάλα είναι το περιεχόμενο της σφαίρας που το
κέντρο της είναι
με την συνήθη μετρική η ανοιχτή μπάλα είναι το περιεχόμενο της σφαίρας που το
κέντρο της είναι 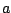 και ακτίνα
και ακτίνα 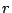 .
.
Η κλειστή μπάλα είναι ολόκληρη σφαίρα με κέντρο 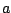 και ακτίνα
και ακτίνα 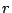 .
.
Ορισμός 1.1.4
Έστω  μετρικός χώρος. Ένα υποσύνολο
μετρικός χώρος. Ένα υποσύνολο 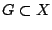 λέγεται
ανοιχτό σύνολο (ως προς την μετρική
λέγεται
ανοιχτό σύνολο (ως προς την μετρική 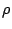 )
αν για κάθε
)
αν για κάθε 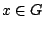 υπάρχει
υπάρχει
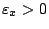 ώστε η ανοιχτή μπάλα με κέντρο
ώστε η ανοιχτή μπάλα με κέντρο 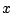 και ακτίνα
και ακτίνα
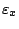 να είναι υποσύνολο του
να είναι υποσύνολο του 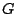 .
.
Παράδειγμα: Το κενό σύνολο είναι ανοιχτό. Το  με συνήθη μετρική είναι ανοιχτό.
με συνήθη μετρική είναι ανοιχτό.
Παράδειγμα: Το σύνολο 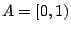 δεν είναι ανοιχτό στο μετρικό χώρο
δεν είναι ανοιχτό στο μετρικό χώρο
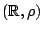 , όπου
, όπου 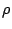 είναι
συνήθης μετρική, γιατί για
είναι
συνήθης μετρική, γιατί για  πρέπει να έχω
πρέπει να έχω
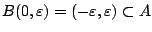 όμως
όμως
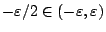 και
και
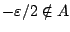 .
.
Πρόταση 1.1.1
Σε κάθε μετρικό χώρο  , κάθε ανοιχτή μπάλα
, κάθε ανοιχτή μπάλα 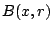 είναι ανοιχτό σύνολο.
είναι ανοιχτό σύνολο.
Απόδειξη: Έστω 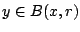 . Τότε
. Τότε 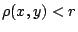 . Οπότε
. Οπότε
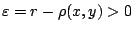 .
Αρκεί να δείξουμε ότι
.
Αρκεί να δείξουμε ότι
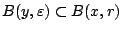 . Έστω
. Έστω
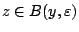 , τότε
, τότε
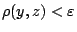 όμως από την ιδιότητα (3) της μετρικής (ορισμός 1.1.1) έχουμε ότι
όμως από την ιδιότητα (3) της μετρικής (ορισμός 1.1.1) έχουμε ότι
 δηλαδή
δηλαδή 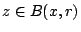 , άρα δείξαμε οτι
, άρα δείξαμε οτι
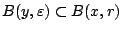 .
.

Πρόταση 1.1.2
Κάθε ανοιχτό σύνολο 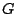 του μετρικού χώρου
του μετρικού χώρου  είναι μια ένωση ανοιχτών μπαλών.
είναι μια ένωση ανοιχτών μπαλών.
Απόδειξη: Για κάθε 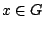 υπάρχει
υπάρχει
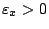 ώστε
ώστε
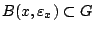 , τότε όμως
, τότε όμως
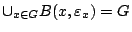

Έστω
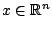 , ορίζουμε την συνήθη νόρμα στο
, ορίζουμε την συνήθη νόρμα στο
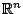 (ή
(ή 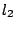 νόρμα) να είναι
νόρμα) να είναι
Πρόταση 1.1.3
Το πλήθος των στοιχείων μιας μπάλας
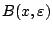 του
του 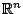 , με τη συνήθη μετρική, είναι
υπεραριθμήσιμο.
, με τη συνήθη μετρική, είναι
υπεραριθμήσιμο.
Απόδειξη: Για κάθε
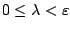 το σημείο
το σημείο
 δηλαδή
δηλαδή
και επιπλέον το σημείο
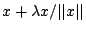 ορίζεται αμφιμονοσήμαντα σε σχέση με το
ορίζεται αμφιμονοσήμαντα σε σχέση με το 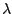 ,
οπότε το πλήθος των σημείων της μπάλας
,
οπότε το πλήθος των σημείων της μπάλας
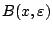 είναι τουλάχιστον ο πληθικός αριθμός του διαστήματος
είναι τουλάχιστον ο πληθικός αριθμός του διαστήματος
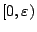 ,
δηλαδή υπεραριθμήσιμο.
,
δηλαδή υπεραριθμήσιμο.

Μερικές βασικές ιδιότητες ανοιχτών υποσυνόλων του μετρικού χώρου 
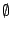 και
και  είναι ανοιχτά.
είναι ανοιχτά.
- Αν
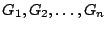 είναι ανοιχτά υποσύνολα του μετρικού χώρου
είναι ανοιχτά υποσύνολα του μετρικού χώρου  τότε και η τομή τους,
τότε και η τομή τους,
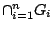 , είναι ανοιχτό σύνολο.
, είναι ανοιχτό σύνολο.
- An
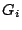 , όπου
, όπου 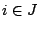 ανοιχτά υποσύνολα του μετρικού χώρου
ανοιχτά υποσύνολα του μετρικού χώρου  τότε και η
ένωσή τους,
τότε και η
ένωσή τους,
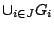 , είναι ανοιχτό σύνολο.
, είναι ανοιχτό σύνολο.
Απόδειξη: Η πρώτη ιδιότητα είναι τετριμμένη. Την δεύτερη ιδιότητα θα την δείξουμε με επαγωγή. Θα δείξουμε πρώτα ότι ισχύει για
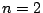 δηλαδή
δηλαδή 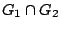 είναι ανοιχτό σύνολο. Έστω
είναι ανοιχτό σύνολο. Έστω
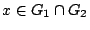 τότε
τότε
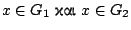 . Αφού
. Αφού 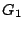 και
και 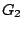 είναι ανοιχτά σύνολα, υπάρχουν
είναι ανοιχτά σύνολα, υπάρχουν
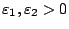 ώστε
ώστε
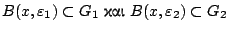 . Θέτουμε
. Θέτουμε
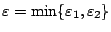 τότε
τότε
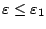 και
και
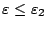 .
.
Άρα 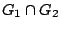 είναι ανοιχτό σύνολο. Υποθέτουμε ότι ισχύει για
είναι ανοιχτό σύνολο. Υποθέτουμε ότι ισχύει για 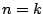 , μένει να δείξουμε ότι ισχύει και για
, μένει να δείξουμε ότι ισχύει και για 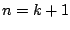 , κάτι που
φαίνεται εύκολα.
, κάτι που
φαίνεται εύκολα.
Τέλος όσο αφορά την τρίτη ιδιότητα έχουμε; έστω
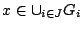 , θα υπάρχει
, θα υπάρχει 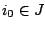 ώστε
ώστε
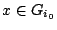 . Αφού το
. Αφού το 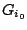 είναι ανοιχτό, υπάρχει
είναι ανοιχτό, υπάρχει
 ώστε
ώστε
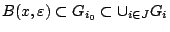 άρα
άρα
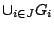 είναι ανοιχτό σύνολο.
είναι ανοιχτό σύνολο.

Στην ιδιότητα δύο μιλάμε για πεπερασμένη τομή (σε αντίθεση με την τρίτη, όπου οι ένωση είναι πάνω σε άπειρα
ανοιχτά υποσύνολα). Το επόμενο παράδειγμα δείχνει οτι η ιδιότητα (2) δεν ισχύει για άπειρη τομή.
Παράδειγμα: Στο μετρικό χώρο  τα υποσύνολα
τα υποσύνολα 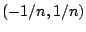 για
για
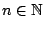 είναι όλα ανοιχτά,
όμως η τομή τους
είναι όλα ανοιχτά,
όμως η τομή τους
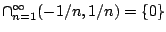 δεν είναι ανοιχτό υποσύνολο του μετρικού
μας χώρου.
δεν είναι ανοιχτό υποσύνολο του μετρικού
μας χώρου.
Νόμοι του De Morgan
Έστω 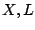 σύνολα και για κάθε
σύνολα και για κάθε 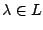 , το
, το 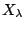 είναι και αυτό σύνολο. Τότε
είναι και αυτό σύνολο. Τότε
-
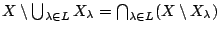
-
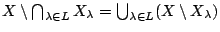
Απόδειξη: (1) Έστω
 αυτό σημαίνει ότι
αυτό σημαίνει ότι  και
και
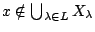 , δηλαδή για κάθε
, δηλαδή για κάθε
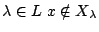 . Ισοδύναμα
. Ισοδύναμα
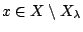 , για κάθε
, για κάθε 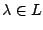 άρα
άρα
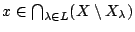
(2)
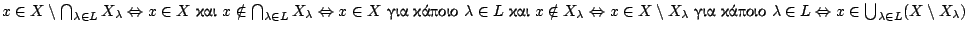

Ορισμός 1.1.5
Έστω  μετρικός χώρος. Ένα υποσύνολο
μετρικός χώρος. Ένα υποσύνολο 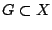 λέγεται
κλειστό σύνολο (ως προς την μετρική
λέγεται
κλειστό σύνολο (ως προς την μετρική 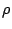 ) αν το συμπλήρωμα του
) αν το συμπλήρωμα του
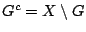 είναι ανοιχτό σύνολο.
είναι ανοιχτό σύνολο.
Παράδειγμα: Το υποσύνολο ![$A=[a,b]$](images/img153.gif) του
του  είναι κλειστό στο μετρικό χώρο
είναι κλειστό στο μετρικό χώρο
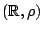 , αφού το
συμπλήρωμά του είναι
, αφού το
συμπλήρωμά του είναι
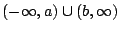 ανοιχτό σύνολο, ως ένωση ανοιχτών συνόλων.
ανοιχτό σύνολο, ως ένωση ανοιχτών συνόλων.
Μερικές βασικές ιδιότητες κλειστών συνόλων του μετρικού χώρου  :
:
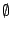 και
και  είναι κλειστά υποσύνολα
είναι κλειστά υποσύνολα
- Αν
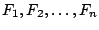 είναι ανοιχτά υποσύνολα του μετρικού χώρου
είναι ανοιχτά υποσύνολα του μετρικού χώρου  τότε και η ένωσή τους,
τότε και η ένωσή τους,
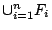 , είναι ανοιχτό σύνολο.
, είναι ανοιχτό σύνολο.
- An
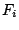 , όπου
, όπου 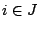 ανοιχτά υποσύνολα του μετρικού χώρου
ανοιχτά υποσύνολα του μετρικού χώρου  τότε και η τομή τους,
τότε και η τομή τους,
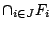 , είναι ανοιχτό σύνολο.
, είναι ανοιχτό σύνολο.
Απόδειξη: Από την στιγμή που το κενό σύνολο είναι συμπλήρωμα του  στο μετρικό χωρο
στο μετρικό χωρο  και αντίστροφα το
και αντίστροφα το  είναι συμπλήρωμα του κενού, μαζί με την πρώτη ιδιότητα των ανοιχτών συνόλων, έπεται ότι είναι κλειστά σύνολα.
είναι συμπλήρωμα του κενού, μαζί με την πρώτη ιδιότητα των ανοιχτών συνόλων, έπεται ότι είναι κλειστά σύνολα.
Τα σύνολα
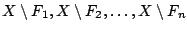 , είναι ανοιχτά, άρα η τομή τους
, είναι ανοιχτά, άρα η τομή τους
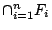 είναι ανοιχτό σύνολο. Οπότε έχουμε
είναι ανοιχτό σύνολο. Οπότε έχουμε
άρα
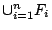 είναι κλειστό σύνολο. Ομοίως αποδεικνύεται η ιδιότητα τρία
είναι κλειστό σύνολο. Ομοίως αποδεικνύεται η ιδιότητα τρία

Άμεση ερμηνεία του ορισμού και μερικά συμπεράσματα που μπορούμε να βγάλουμε είναι ότι το εσωτερικό ενός
συνόλου  είναι πάντα ανοιχτό σύνολο. Δεν υπερβαίνει ποτέ το ίδιο το σύνολο, δηλαδή είναι πάντα υποσύνολο
του
είναι πάντα ανοιχτό σύνολο. Δεν υπερβαίνει ποτέ το ίδιο το σύνολο, δηλαδή είναι πάντα υποσύνολο
του  (αν και μπορεί να ισούται με το ίδιο το
(αν και μπορεί να ισούται με το ίδιο το  ). Είναι το μεγαλύτερο ανοιχτό υποσύνολό του και όλα τα
ανοιχτά υποσύνολα του
). Είναι το μεγαλύτερο ανοιχτό υποσύνολό του και όλα τα
ανοιχτά υποσύνολα του  περιέχονται στο
περιέχονται στο 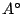 .
.
Παράδειγμα:
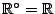 ,
,
![$(a,b]^{\circ}=(a,b)$](images/img166.gif) ,
,
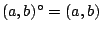 ,
,
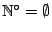 ,
,
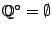
Παράδειγμα: Οποιοδήποτε αριθμήσιμο ή πεπερασμένου πλήθους στοιχείων υποσύνολο  του
του  έχει κενό
εσωτερικό σύνολο.
έχει κενό
εσωτερικό σύνολο.
Όπως και στην περίπτωση του εσωτερικού συνόλου έτσι και εδώ μπορούμε να βγάλουμε κάποια χρήσιμα
συμπεράσματα. Η κλειστότητα ενός συνόλου  είναι κλειστό σύνολο που πάντα περιέχει το
είναι κλειστό σύνολο που πάντα περιέχει το  .
Η κλειστότητα είναι το μικρότερο κλειστό σύνολο που περιέχει το
.
Η κλειστότητα είναι το μικρότερο κλειστό σύνολο που περιέχει το  . Το
. Το  είναι κλειστό σύνολο
αν και μόνο αν είναι ίσο με την κλειστότητα του,
είναι κλειστό σύνολο
αν και μόνο αν είναι ίσο με την κλειστότητα του,
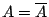 .
.
Παράδειγμα: Η κλειστότητα των ρητών αριθμών είναι όλο το  ,
,
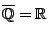 .
.
Θεώρημα 1.1.1
Έστω  ένας μετρικός χώρος και
ένας μετρικός χώρος και 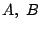 υποσύνολα του
υποσύνολα του  . Τότε ισχύουν τα παρακάτω:
. Τότε ισχύουν τα παρακάτω:
-
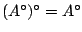 και
και
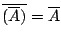
-
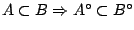 και
και
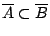
-
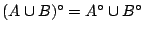 και
και
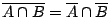
Η πρόταση (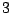 ) ισχύει και για πεπερασμένες τομές και ενώσεις αντίστοιχα.
) ισχύει και για πεπερασμένες τομές και ενώσεις αντίστοιχα.
Θεώρημα 1.1.2
Έστω  ένας μετρικός χώρος και
ένας μετρικός χώρος και 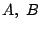 ένα υποσύνολο του
ένα υποσύνολο του  . Τότε ισχύουν τα ακόλουθα
. Τότε ισχύουν τα ακόλουθα
- Αν
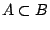 τότε
τότε 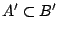
-
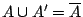
-
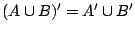
Η πρόταση (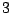 ) ισχύει και για πεπερασμένες ενώσεις
) ισχύει και για πεπερασμένες ενώσεις
Ορισμός 1.1.12
Έστω  ένα υποσύνολο ενός μετρικού χώρου
ένα υποσύνολο ενός μετρικού χώρου  . Θα λέμε ότι το σύνολο
. Θα λέμε ότι το σύνολο  είναι
πυκνό υποσύνολο του
είναι
πυκνό υποσύνολο του  αν για κάθε
αν για κάθε  ισχύει ότι για
κάθε
ισχύει ότι για
κάθε  υπάρχει
υπάρχει 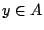 ώστε
ώστε
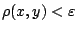
Πρόταση 1.1.4
Ένα υποσύνολο  ενός μετρικού χώρου
ενός μετρικού χώρου  είναι πυκνό υποσύνολο του
είναι πυκνό υποσύνολο του  αν και μόνο αν
αν και μόνο αν
Απόδειξη: Αρχικά θεωρούμε ότι το σύνολο  είναι πυκνό υποσύνολο του
είναι πυκνό υποσύνολο του  . Τότε για τυχόν
. Τότε για τυχόν  έχουμε ότι για
κάθε
έχουμε ότι για
κάθε
 υπάρχει
υπάρχει 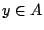 ώστε
ώστε
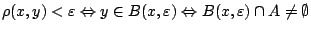 . Αυτό σημαίνει ότι αν
. Αυτό σημαίνει ότι αν
 τότε
τότε 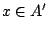 άρα
άρα 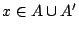 δηλαδή
δηλαδή
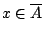 . Άρα
. Άρα
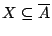 ,
δηλαδή
,
δηλαδή
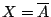 .
.
Αντίστροφα, έστω ότι ισχύει
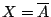 . Θεωρούμε τυχόν
. Θεωρούμε τυχόν  και τυχόν
και τυχόν
 . Αν
. Αν
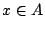 τότε υπάρχει
τότε υπάρχει 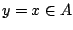 ώστε
ώστε
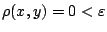 , οπότε υποθέτουμε ότι
, οπότε υποθέτουμε ότι  (αλλά
(αλλά
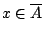 ). Θέλουμε να δείξουμε ότι υπάρχει
). Θέλουμε να δείξουμε ότι υπάρχει 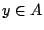 ώστε
ώστε
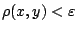 . Έστω ότι δεν
υπάρχει (για να καταλήξουμε σε άτοπο) τέτοιο
. Έστω ότι δεν
υπάρχει (για να καταλήξουμε σε άτοπο) τέτοιο 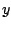 , αυτό σημαίνει ότι υπάρχει
, αυτό σημαίνει ότι υπάρχει 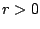 ώστε η ανοιχτή μπάλα με
κέντρο
ώστε η ανοιχτή μπάλα με
κέντρο 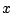 και ακτίνα
και ακτίνα 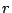 δεν τέμνει καθόλου το
δεν τέμνει καθόλου το  (
(
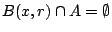 ), άρα
), άρα
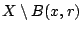 είναι κλειστό υπερσύνολο του
είναι κλειστό υπερσύνολο του  , τότε όμως
, τότε όμως
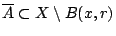 , άτοπο αφού
, άτοπο αφού
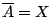 .
.
Άρα  είναι πυκνό σύνολο του
είναι πυκνό σύνολο του 






Next: Συνέχεια Συναρτήσεων
Up: Μετρικοί Χώροι
Previous: Μετρικοί Χώροι
Contents
Index
Khusainov Alexander
2002-10-25
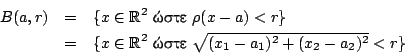
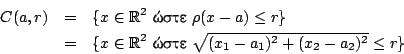
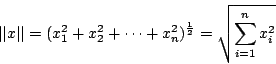
![]()
![]() , θα υπάρχει
, θα υπάρχει ![]() ώστε
ώστε
![]() . Αφού το
. Αφού το ![]() είναι ανοιχτό, υπάρχει
είναι ανοιχτό, υπάρχει
![]() ώστε
ώστε
![]() άρα
άρα
![]() είναι ανοιχτό σύνολο.
είναι ανοιχτό σύνολο.
![]()
![]() τα υποσύνολα
τα υποσύνολα ![]() για
για
![]() είναι όλα ανοιχτά,
όμως η τομή τους
είναι όλα ανοιχτά,
όμως η τομή τους
![]() δεν είναι ανοιχτό υποσύνολο του μετρικού
μας χώρου.
δεν είναι ανοιχτό υποσύνολο του μετρικού
μας χώρου.
![]() σύνολα και για κάθε
σύνολα και για κάθε ![]() , το
, το ![]() είναι και αυτό σύνολο. Τότε
είναι και αυτό σύνολο. Τότε
![]()
![]()
![]() του
του ![]() είναι κλειστό στο μετρικό χώρο
είναι κλειστό στο μετρικό χώρο
![]() , αφού το
συμπλήρωμά του είναι
, αφού το
συμπλήρωμά του είναι
![]() ανοιχτό σύνολο, ως ένωση ανοιχτών συνόλων.
ανοιχτό σύνολο, ως ένωση ανοιχτών συνόλων.
![]() :
:
![]() , είναι ανοιχτά, άρα η τομή τους
, είναι ανοιχτά, άρα η τομή τους
![]() είναι ανοιχτό σύνολο. Οπότε έχουμε
είναι ανοιχτό σύνολο. Οπότε έχουμε
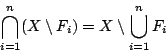
![]() είναι πάντα ανοιχτό σύνολο. Δεν υπερβαίνει ποτέ το ίδιο το σύνολο, δηλαδή είναι πάντα υποσύνολο
του
είναι πάντα ανοιχτό σύνολο. Δεν υπερβαίνει ποτέ το ίδιο το σύνολο, δηλαδή είναι πάντα υποσύνολο
του ![]() (αν και μπορεί να ισούται με το ίδιο το
(αν και μπορεί να ισούται με το ίδιο το ![]() ). Είναι το μεγαλύτερο ανοιχτό υποσύνολό του και όλα τα
ανοιχτά υποσύνολα του
). Είναι το μεγαλύτερο ανοιχτό υποσύνολό του και όλα τα
ανοιχτά υποσύνολα του ![]() περιέχονται στο
περιέχονται στο ![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() του
του ![]() έχει κενό
εσωτερικό σύνολο.
έχει κενό
εσωτερικό σύνολο.
![]() είναι κλειστό σύνολο που πάντα περιέχει το
είναι κλειστό σύνολο που πάντα περιέχει το ![]() .
Η κλειστότητα είναι το μικρότερο κλειστό σύνολο που περιέχει το
.
Η κλειστότητα είναι το μικρότερο κλειστό σύνολο που περιέχει το ![]() . Το
. Το ![]() είναι κλειστό σύνολο
αν και μόνο αν είναι ίσο με την κλειστότητα του,
είναι κλειστό σύνολο
αν και μόνο αν είναι ίσο με την κλειστότητα του,
![]() .
.
![]() ,
,
![]() .
.
![]() . Θεωρούμε τυχόν
. Θεωρούμε τυχόν ![]() και τυχόν
και τυχόν
![]() . Αν
. Αν
![]() τότε υπάρχει
τότε υπάρχει ![]() ώστε
ώστε
![]() , οπότε υποθέτουμε ότι
, οπότε υποθέτουμε ότι ![]() (αλλά
(αλλά
![]() ). Θέλουμε να δείξουμε ότι υπάρχει
). Θέλουμε να δείξουμε ότι υπάρχει ![]() ώστε
ώστε
![]() . Έστω ότι δεν
υπάρχει (για να καταλήξουμε σε άτοπο) τέτοιο
. Έστω ότι δεν
υπάρχει (για να καταλήξουμε σε άτοπο) τέτοιο ![]() , αυτό σημαίνει ότι υπάρχει
, αυτό σημαίνει ότι υπάρχει ![]() ώστε η ανοιχτή μπάλα με
κέντρο
ώστε η ανοιχτή μπάλα με
κέντρο ![]() και ακτίνα
και ακτίνα ![]() δεν τέμνει καθόλου το
δεν τέμνει καθόλου το ![]() (
(
![]() ), άρα
), άρα
![]() είναι κλειστό υπερσύνολο του
είναι κλειστό υπερσύνολο του ![]() , τότε όμως
, τότε όμως
![]() , άτοπο αφού
, άτοπο αφού
![]() .
.
![]() είναι πυκνό σύνολο του
είναι πυκνό σύνολο του ![]()
![]()