




Next: Τοπολογία Μετρικού Χώρου
Up: Μετρική Τοπολογία
Previous: Μετρική Τοπολογία
Contents
Index
Ορισμός 1.1.1
Έστω Χ ένα σύνολο, μια συνάρτηση
![$\rho:X\times X\rightarrow
[0,\infty]$](images/img28.gif) θα λέγεται μετρική αν ισχύουν οι παρακάτω
συνθήκες:
θα λέγεται μετρική αν ισχύουν οι παρακάτω
συνθήκες:
-
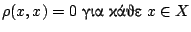
-
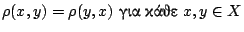 (συμμετρία)
(συμμετρία)
-
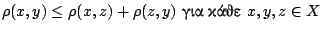 (τριγωνική ανισότητα)
(τριγωνική ανισότητα)
Έπιπλέον το  εφοδιασμένο με την μετρική
εφοδιασμένο με την μετρική 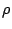 θα λέγεται
μετρικός χώρος και θα το
συμβολίζουμε
θα λέγεται
μετρικός χώρος και θα το
συμβολίζουμε  και εφόσον δεν υπάρχει πρόβλημα στο να μπερδέψουμε
τις μετρικές θα γράφουμε μόνο
και εφόσον δεν υπάρχει πρόβλημα στο να μπερδέψουμε
τις μετρικές θα γράφουμε μόνο  .
.
Μερικά παραδείγματα
Παράδειγμα: Στο  η συνήθης ή
Ευκλείδεια μετρική ορίζεται να είναι
η συνάρτηση:
η συνήθης ή
Ευκλείδεια μετρική ορίζεται να είναι
η συνάρτηση:
όπου
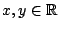
Το ότι η συνάρτηση 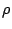 είναι μετρική στο
είναι μετρική στο  φαίνεται άμεσα (αφού ισχύουν και οι
τρεις συνθήκες του ορισμού).
φαίνεται άμεσα (αφού ισχύουν και οι
τρεις συνθήκες του ορισμού).
Παράδειγμα: Στο 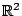 η συνήθης ή Ευκλείδεια μετρική ορίζεται να είναι η συνάρτηση:
η συνήθης ή Ευκλείδεια μετρική ορίζεται να είναι η συνάρτηση:
όπου
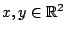 , δηλαδή
, δηλαδή 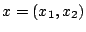 και
και 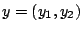 με
με
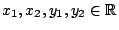 .
.
Παράδειγμα: Στο 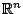 η συνήθης ή
Ευκλείδεια μετρική ορίζεται να είναι
η συνάρτηση:
η συνήθης ή
Ευκλείδεια μετρική ορίζεται να είναι
η συνάρτηση:
όπου
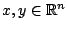
Παράδειγμα: Αν  είναι τυχόν μη κενό σύνολο, η συνάρτηση
είναι τυχόν μη κενό σύνολο, η συνάρτηση
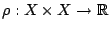 με τύπο
με τύπο
είναι μετρική στο  και λέγεται
διακριτή μετρική
και λέγεται
διακριτή μετρική
Απόδειξη: Οι δύο πρώτες ιδιότητες της μετρικής προκύπτουν άμεσα από τον ορισμό της 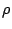 . Έτσι αρκεί να δείξουμε ότι
για τυχόντα στοιχεία
. Έτσι αρκεί να δείξουμε ότι
για τυχόντα στοιχεία
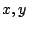 και
και 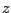 του
του  ισχύει
ισχύει
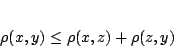 |
(1.1) |
Επειδή οι τιμές των αποστάσεων
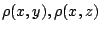 και
και 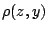 είναι
είναι 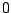 ή
ή 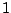 , η μόνη περίπτωση όπου δεν θα
ίσχυε η σχέση 1.1, θα ήταν η περίπτωση όπου
, η μόνη περίπτωση όπου δεν θα
ίσχυε η σχέση 1.1, θα ήταν η περίπτωση όπου 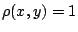 και
και
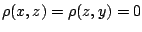 . Αλλά τότε, από
τον ορισμό της
. Αλλά τότε, από
τον ορισμό της 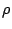 , θα είχαμε
, θα είχαμε
και ταυτόχρονα
που είναι άτοπο.

Μπορούμε να γενικεύσουμε την τριγωνική ανισότητα. Έστω
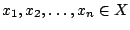 όπου
όπου  μετρικός χώρος
και
μετρικός χώρος
και 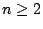 τότε
τότε
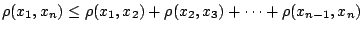 .
.
Απόδειξη: Για 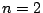 , ο ισχυρισμός ισχύει από τον ορισμό. Έστω ότι ισχύει για
, ο ισχυρισμός ισχύει από τον ορισμό. Έστω ότι ισχύει για 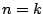 , δηλαδή
, δηλαδή
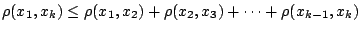 . Βάσει μαθηματικής
επαγωγής αρκεί να δείξουμε ότι ισχύει για
. Βάσει μαθηματικής
επαγωγής αρκεί να δείξουμε ότι ισχύει για 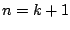 . Κάτι που ισχύει αφού
. Κάτι που ισχύει αφού
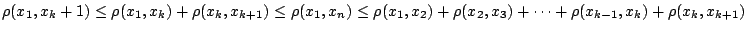 .
.

Subsections





Next: Τοπολογία Μετρικού Χώρου
Up: Μετρική Τοπολογία
Previous: Μετρική Τοπολογία
Contents
Index
Khusainov Alexander
2002-10-25
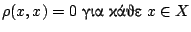
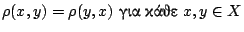 (συμμετρία)
(συμμετρία)
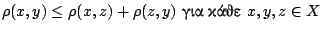 (τριγωνική ανισότητα)
(τριγωνική ανισότητα)
![]() η συνήθης ή
Ευκλείδεια μετρική ορίζεται να είναι
η συνάρτηση:
η συνήθης ή
Ευκλείδεια μετρική ορίζεται να είναι
η συνάρτηση:
![]() είναι μετρική στο
είναι μετρική στο ![]() φαίνεται άμεσα (αφού ισχύουν και οι
τρεις συνθήκες του ορισμού).
φαίνεται άμεσα (αφού ισχύουν και οι
τρεις συνθήκες του ορισμού).
![]() η συνήθης ή Ευκλείδεια μετρική ορίζεται να είναι η συνάρτηση:
η συνήθης ή Ευκλείδεια μετρική ορίζεται να είναι η συνάρτηση:
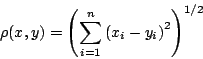
![]() όπου
όπου ![]() μετρικός χώρος
και
μετρικός χώρος
και ![]() τότε
τότε
![]() .
.
![]() , ο ισχυρισμός ισχύει από τον ορισμό. Έστω ότι ισχύει για
, ο ισχυρισμός ισχύει από τον ορισμό. Έστω ότι ισχύει για ![]() , δηλαδή
, δηλαδή
![]() . Βάσει μαθηματικής
επαγωγής αρκεί να δείξουμε ότι ισχύει για
. Βάσει μαθηματικής
επαγωγής αρκεί να δείξουμε ότι ισχύει για ![]() . Κάτι που ισχύει αφού
. Κάτι που ισχύει αφού
![]() .
.
![]()