- Αν
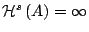 τότε
τότε 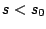
- Αν
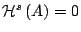 τότε
τότε 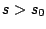
Μιλώντας μη αυστηρά η διάσταση Hausdorff ενός συνόλου
![]() είναι το σημείο όπου η γραφική παράσταση του
είναι το σημείο όπου η γραφική παράσταση του
![]() (προσοχή
συναρτήσει του
(προσοχή
συναρτήσει του ![]() και όχι του
και όχι του ![]() ) κάνει το άλμα από το άπειρο στο μηδέν,
σχήμα 3.1.
) κάνει το άλμα από το άπειρο στο μηδέν,
σχήμα 3.1.
Απόδειξη: Έστω
![\begin{eqnarray*}
\mathop{\operator@font diam}(f[A]) &=& \sup \{\rho \left( f(x...
...t)\}\\
&=& \sup \{r \rho(x,y) \}\\
&=& r \sup\{\rho(x,y) \}
\end{eqnarray*}](images/img1369.gif)
Τώρα, έστω ότι
![]() είναι μια
είναι μια ![]() -κάλυψη του
-κάλυψη του ![]() . Τότε υπάρχει
. Τότε υπάρχει ![]()
![]() -κάλυψη του
-κάλυψη του ![]() και αντίστροφα. Από τον ορισμό έχουμε
και αντίστροφα. Από τον ορισμό έχουμε
![\begin{eqnarray*}
\mathcal{H}^s_{\varepsilon r}(f[F]) &=& \inf \{\sum_{f[A_i]\i...
...or@font diam}A_i)^s\}\\
&=& r^s \mathcal{H}^s_\varepsilon (F)
\end{eqnarray*}](images/img1376.gif)
(2) Έστω
![]() , τότε
, τότε ![]() άρα
άρα
![]() . Όμως
. Όμως
![]() , τότε
, τότε
![]() . Έπεται
. Έπεται
![]() . Αυτό ισχύει για όλα
. Αυτό ισχύει για όλα
![]() άρα έχουμε
άρα έχουμε
![]() .
.
![]() και
και
![]() από την (1) έχουμε
από την (1) έχουμε
![]() .
.
![]()
Σύνολα Cantor.
Θα μελετήσουμε τώρα την διάσταση Hausdorff του συνόλου Cantor ![]() .
Βάσει του ορισμού του μέτρου Hausdorff , είναι
σχετικά πιο εύκολο να βρούμε το άνω φράγμα του, παρά το κάτω. Μια ((καλή)) κάλυψη του συνόλου,
θα μας δώσει μια εκτίμηση του άνω φράγματος.
.
Βάσει του ορισμού του μέτρου Hausdorff , είναι
σχετικά πιο εύκολο να βρούμε το άνω φράγμα του, παρά το κάτω. Μια ((καλή)) κάλυψη του συνόλου,
θα μας δώσει μια εκτίμηση του άνω φράγματος.
Από τον ορισμό 1.5.7 του συνόλου Cantor έχουμε ότι
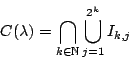

Υπενθυμίζουμε ότι ο συμβολισμός των διαστημάτων ![]() προέρχεται από την κατασκευή του
συνόλου Cantor στον ορισμό 1.5.7.
προέρχεται από την κατασκευή του
συνόλου Cantor στον ορισμό 1.5.7.
Θα δείξουμε τώρα ότι για οποιοδήποτε ανοιχτό διάστημα ![]() και δοσμένο
και δοσμένο ![]() ισχύει
ισχύει
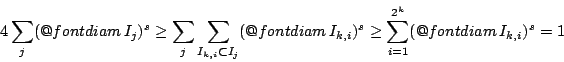
Τώρα όσον αφορά την 3.4, υποθέτουμε ότι υπάρχουν κάποια ![]() υποσύνολα του
υποσύνολα του
![]() . Έστω
. Έστω ![]() είναι εκείνο το βήμα για το οποίο κάποια από τα διαστήματα
είναι εκείνο το βήμα για το οποίο κάποια από τα διαστήματα ![]() περιέχονται
στο
περιέχονται
στο ![]() . Τότε
. Τότε ![]() και τα διαστήματα
και τα διαστήματα ![]() που τέμνουν το
που τέμνουν το ![]() (προσοχή όχι μόνο
εκείνα που περιέχονται εξ'' ολοκλήρου στο
(προσοχή όχι μόνο
εκείνα που περιέχονται εξ'' ολοκλήρου στο ![]() ) είναι το πολύ
) είναι το πολύ ![]() , ειδάλλως το
, ειδάλλως το ![]() θα
περιείχε κάποια από τα διαστήματα του προηγουμένου βήματος
θα
περιείχε κάποια από τα διαστήματα του προηγουμένου βήματος ![]() . Έτσι για
. Έτσι για ![]() έχουμε
έχουμε

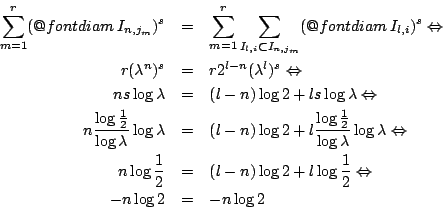
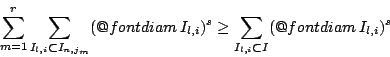
Παρατηρούμε ότι η διάσταση Hausdorff των συνόλων Cantor , ![]() ,
((μετράει)) με φυσικό τρόπο τα μεγέθη τους. Όταν το
,
((μετράει)) με φυσικό τρόπο τα μεγέθη τους. Όταν το ![]() αυξάνεται, το μηκος των διαγραμμένων
διαστημάτων μειώνεται και το σύνολο Cantor ((μεγαλώνει)) και παράλληλα μεγαλώνει η
αυξάνεται, το μηκος των διαγραμμένων
διαστημάτων μειώνεται και το σύνολο Cantor ((μεγαλώνει)) και παράλληλα μεγαλώνει η
![]() . Επίσης αν αφήσουμε το
. Επίσης αν αφήσουμε το ![]() να διατρέξει από
να διατρέξει από ![]() ως το
ως το ![]() , η
, η
![]() θα πάρει τις τιμές από
θα πάρει τις τιμές από ![]() ως το
ως το ![]() .
.
Έστω τώρα ότι
![]() τότε
τότε
![]() και
και
![]() ,
όμως αυτό σημαίνει ότι
,
όμως αυτό σημαίνει ότι
![]() για όλα τα
για όλα τα
![]() , άρα
, άρα
![]() .
.
![]()
Γενικά η διάσταση Hausdorff ενός συνόλου, μόνη της δεν μας δίνει και πολλές πληροφορίες
σχετικά με τις τοπολογικές ιδιότητες του συνόλου. Όμως αν η διάσταση Hausdorff είναι
μικρότερη του ![]() τότε το σύνολο θα πρέπει να είναι τόσο αραιό ώστε να μην είναι ούτε καν τοπικά
συνεκτικό.
τότε το σύνολο θα πρέπει να είναι τόσο αραιό ώστε να μην είναι ούτε καν τοπικά
συνεκτικό.
Σκόνη Cantor
Έστω ένα τετράγωνο πλευράς ![]() . Σε κάθε στάδιο της κατασκευής, τα τετράγωνα χωρίζονται σε 16
τετράγωνα με μήκος ακμής 1/4 του μήκους ακμής, από τα οποία τέσσερα του ((ίδιου σχεδίου))
παραμένουν, έτσι ώστε η προβολή τους στο άξονα
. Σε κάθε στάδιο της κατασκευής, τα τετράγωνα χωρίζονται σε 16
τετράγωνα με μήκος ακμής 1/4 του μήκους ακμής, από τα οποία τέσσερα του ((ίδιου σχεδίου))
παραμένουν, έτσι ώστε η προβολή τους στο άξονα ![]() να καλύπτει διάστημα μήκους
να καλύπτει διάστημα μήκους ![]() .
Μετά από άπειρα στάδια πέρνουμε το σύνολο
.
Μετά από άπειρα στάδια πέρνουμε το σύνολο ![]() το οποίο και το λέμε ((σκόνη Cantor)),
σχήμα 3.2. Θα εξετάσουμε στην συνέχεια την διάσταση Hausdorff του
το οποίο και το λέμε ((σκόνη Cantor)),
σχήμα 3.2. Θα εξετάσουμε στην συνέχεια την διάσταση Hausdorff του ![]() .
.
Παίρνοντας την προφανή κάλυψη του ![]() που αποτελείται από
που αποτελείται από ![]() τετράγωνα πλευράς
τετράγωνα πλευράς ![]() ,
δηλαδή διαμέτρου
,
δηλαδή διαμέτρου
![]() , στο
, στο ![]() , όπου
, όπου ![]() είναι το
είναι το ![]() -οστό στάδιο
της κατασκευής, έχουμε μια εκτίμηση του
-οστό στάδιο
της κατασκευής, έχουμε μια εκτίμηση του
![]() .
Για
.
Για
![]() το
το
![]() άρα
άρα
Έστω η συνάρτηση ![]() είναι ορθοκανονική προβολή του
είναι ορθοκανονική προβολή του ![]() στον άξονα
στον άξονα ![]() . Η ορθοκανονική προβολή δεν
μεγάλωνει τις αποστάσεις, δηλαδή
. Η ορθοκανονική προβολή δεν
μεγάλωνει τις αποστάσεις, δηλαδή
![]() αν
αν
![]() , άρα
, άρα ![]() ικανοποιεί την
συνθήκη Lipschitz. Βάσει της κατασκευής η προβολή του
ικανοποιεί την
συνθήκη Lipschitz. Βάσει της κατασκευής η προβολή του ![]() στον άξονα
στον άξονα ![]() θα είναι
διάστημα
θα είναι
διάστημα ![]() , σχήμα 3.2. Από την πρόταση 3.2.1
, σχήμα 3.2. Από την πρόταση 3.2.1
Το ((κόλπο)) που χρησιμοποιήσαμε την προβολή για να πάρουμε την κάτω εκτίμηση, δουλεύει μόνο σε συγκεκριμένες περιπτώσεις και δεν αποτελεί βάση για μια πιό γενική μέθοδο.