




Next: Διάσταση Hausdorff
Up: Διάσταση Hausdorff
Previous: Διάσταση Hausdorff
Contents
Index
Ορισμός 3.1.1
Έστω  μετρικός χώρος. Έστω θετικός αριθμός
μετρικός χώρος. Έστω θετικός αριθμός 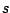 , υποψήφιος
αριθμός για την διάσταση. Το
, υποψήφιος
αριθμός για την διάσταση. Το 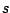 -διάστατο εξωτερικό μέτρο
Hausdorff , συμβολισμός
-διάστατο εξωτερικό μέτρο
Hausdorff , συμβολισμός
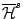 , είναι το εξωτερικό μέτρο της Μεθόδου
ΙΙ ορισμένο από την σύνολό συνάρτηση
, είναι το εξωτερικό μέτρο της Μεθόδου
ΙΙ ορισμένο από την σύνολό συνάρτηση
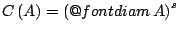 .
.
Ας δούμε αναλυτικότερα τον ορισμό. Μια οικογένεια 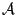 υποσυνόλων του
υποσυνόλων του  , καλείται αριθμήσιμη κάλυψη του συνόλου
, καλείται αριθμήσιμη κάλυψη του συνόλου 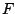 αν και μόνο αν
αν και μόνο αν
και 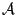 είναι αριθμήσιμη (ενδεχομένως και
πεπερασμένη) οικογένεια των συνόλων. Έστω
είναι αριθμήσιμη (ενδεχομένως και
πεπερασμένη) οικογένεια των συνόλων. Έστω 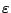 θετικός (πολύ μικρός). Η κάλυψη
θετικός (πολύ μικρός). Η κάλυψη
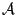 λέγεται
λέγεται 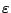 -
κάλυψη αν και μόνο αν
-
κάλυψη αν και μόνο αν
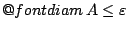 για όλα τα
για όλα τα
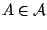 . Ορίζουμε
. Ορίζουμε
όπου το κάτω πέρας (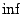 ) είναι πάνω απ'' όλες τις αριθμήσιμες
) είναι πάνω απ'' όλες τις αριθμήσιμες
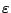 -καλύψεις
-καλύψεις 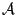 του συνόλου
του συνόλου 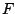 . Κατά συμφωνία
. Κατά συμφωνία
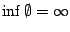 , δηλαδή αν δεν υπάρχει καμία αριθμήσιμη
, δηλαδή αν δεν υπάρχει καμία αριθμήσιμη 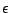 -κάλυψη
-κάλυψη
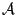 του
του 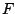 , τότε
, τότε
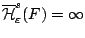 .
.
Ένας απλός υπολογισμός δείχνει πως όταν το 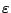 μειώνεται, το
μειώνεται, το
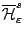 αυξάνεται. Τέλος
αυξάνεται. Τέλος
είναι το
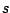 -διάστατο εξωτερικό μέτρο Hausdorff του συνόλου
-διάστατο εξωτερικό μέτρο Hausdorff του συνόλου
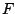
Ο περιορισμός του
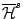 σε μετρήσιμα
υποσύνολα του
σε μετρήσιμα
υποσύνολα του  είναι s-διάστατο μέτρο
Hausdorff, και γράφεται
είναι s-διάστατο μέτρο
Hausdorff, και γράφεται
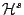 .
.
Είναι ενδιαφέρον να δούμε την συμπεριφορά του 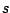 -διάστατου μέτρου
Hausdorff συναρτήσει του
-διάστατου μέτρου
Hausdorff συναρτήσει του 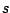 . Βάσει του
επόμενου θεωρήματος μπορούμε να την ζωγραφίσουμε όπως στο σχήμα
3.1.
. Βάσει του
επόμενου θεωρήματος μπορούμε να την ζωγραφίσουμε όπως στο σχήμα
3.1.
Θεώρημα 3.1.1
Έστω 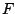 σύνολο Borel και έστω
σύνολο Borel και έστω 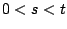 , τότε εάν
, τότε εάν
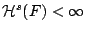 έχουμε ότι
έχουμε ότι
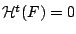 και εάν
και εάν
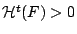 έχουμε ότι
έχουμε ότι
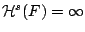 .
.
Απόδειξη: Έστω ένα σύνολο  με
με
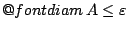 τότε αφού
τότε αφού 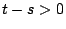 , έχουμε ότι
, έχουμε ότι
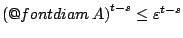 ,
τότε όμως
,
τότε όμως
 |
(3.1) |
Κάθε 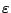 -κάλυψη,
-κάλυψη, 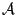 του συνόλου
του συνόλου 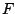 αποτελείται από κάποια τέτοια
αποτελείται από κάποια τέτοια  , και
, και
Από τον ορισμό όμως η κάλυψη 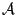 είναι αριθμήσιμη οπότε η ανισότητα
3.1 επάγει
είναι αριθμήσιμη οπότε η ανισότητα
3.1 επάγει
για όλες τις αριθμήσιμες 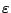 -καλύψεις
-καλύψεις 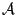 του συνόλου
του συνόλου  . Άρα
. Άρα
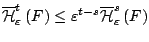 για όλα τα σύνολα
για όλα τα σύνολα 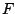 . Tώρα αν
. Tώρα αν
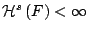 ,
τότε
,
τότε
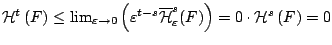 δηλαδή
δηλαδή
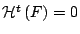 (αφού το μέτρο δεν μπορεί να είναι
αρνητικό).
(αφού το μέτρο δεν μπορεί να είναι
αρνητικό).
Για να αποδείξουμε την άλλη κατεύθυνση του θεωρήματος θα
ακολουθήσουμε την ίδια λογική. Έχουμε
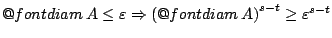 ,
αφού
,
αφού 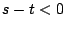 . Τότε έχουμε
. Τότε έχουμε
και
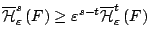 για όλα τα σύνολα
για όλα τα σύνολα 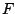 . Tώρα αν
. Tώρα αν
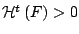 , τότε
, τότε
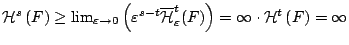 δηλαδή
δηλαδή
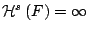

Πρόταση 3.1.1
Αν 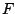 είναι ένα πεπερασμένο σύνολο, τότε το
είναι ένα πεπερασμένο σύνολο, τότε το 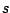 -διάστατο μέτρο Hausdorff του είναι μηδέν για όλα τα
-διάστατο μέτρο Hausdorff του είναι μηδέν για όλα τα 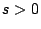 .
.

Απόδειξη: Αφού το 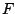 είναι πεπερασμένο σύνολο, μπορούμε να πάρουμε την κάλυψη
είναι πεπερασμένο σύνολο, μπορούμε να πάρουμε την κάλυψη 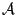 που να αποτελείται από
πεπερασμένα το πλήθος μονοσύνολα,
τα στοιχεία των οποίων είναι αυτά του συνόλου
που να αποτελείται από
πεπερασμένα το πλήθος μονοσύνολα,
τα στοιχεία των οποίων είναι αυτά του συνόλου 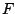 . Τώρα η διάμετρος του μονοσυνόλου είναι μηδέν, άρα
. Τώρα η διάμετρος του μονοσυνόλου είναι μηδέν, άρα
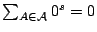 . Επιπλέον, έχοντας ορίσει το μέτρο ως μη αρνητική συνάρτηση και εφόσον θέλουμε το κάτω πέρας συνεπάγεται
. Επιπλέον, έχοντας ορίσει το μέτρο ως μη αρνητική συνάρτηση και εφόσον θέλουμε το κάτω πέρας συνεπάγεται
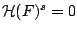 για όλα τα
για όλα τα 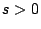

Ας δούμε μερικά παραδείγματα του μέτρου Hausdorff . Έστω 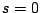 . Είναι αντιληπτό ότι
το μηδέν-διάστατο μέτρο Hausdorff ενός συνόλου στην ουσία μας λέει από πόσα στοιχεία
αποτελείται το σύνολο.
. Είναι αντιληπτό ότι
το μηδέν-διάστατο μέτρο Hausdorff ενός συνόλου στην ουσία μας λέει από πόσα στοιχεία
αποτελείται το σύνολο.
Στην συνέχεια, έστω 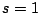 . Το μονο-διάστατο μέτρο Hausdorff ερμηνεύεται ως γενικευμένο
μέτρο που μετράει μήκος, οπως έχουμε πει και για το μέτρο Lebesgue στο
. Το μονο-διάστατο μέτρο Hausdorff ερμηνεύεται ως γενικευμένο
μέτρο που μετράει μήκος, οπως έχουμε πει και για το μέτρο Lebesgue στο  .
Για τη ακρίβεια
.
Για τη ακρίβεια
Θεώρημα 3.1.2
Το μέτρο Lebesgue ταυτίζεται με το μονο-διάστατο μέτρο Hausdorff 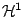 στο
στο  .
.
Απόδειξη: Έστω σύνολο
 .
Είναι φανερό ότι για
.
Είναι φανερό ότι για
 το σύνολο
το σύνολο
είναι υποσύνολο του συνόλου
Βάσει του ορισμού το κάτω πέρας του συνόλου 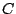 είναι το
εξωτερικό μέτρο Lebesgue του συνόλου
είναι το
εξωτερικό μέτρο Lebesgue του συνόλου 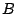 , όπως και
, όπως και
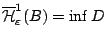 ,
επειδή όμως για κάθε
,
επειδή όμως για κάθε 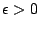 ,
, 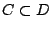 έχουμε ότι
έχουμε ότι
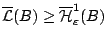 .
Οπότε και
.
Οπότε και
 .
.
Τώρα, έστω ότι σύνολο
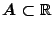 έχει πεπερασμένη διάμετρο
έχει πεπερασμένη διάμετρο 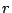 , τότε
, τότε
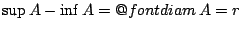 ,
άρα το
,
άρα το  περιέχεται σ'' ένα κλειστό διαστημα
περιέχεται σ'' ένα κλειστό διαστημα 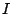 μήκους
μήκους 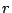 και ισχύει
και ισχύει
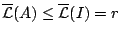 . Από την σ-υποπροσθετικότητα του εξωτερικού μέτρου Lebesgue ,
έχουμε
. Από την σ-υποπροσθετικότητα του εξωτερικού μέτρου Lebesgue ,
έχουμε
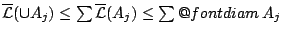 ,
αυτό ισχύει για όλες τις οικογένειες με σύνολα διαμέτρου μικρότερο από το
,
αυτό ισχύει για όλες τις οικογένειες με σύνολα διαμέτρου μικρότερο από το 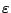 .
Από την μονοτονία του μέτρου έχουμε,
.
Από την μονοτονία του μέτρου έχουμε,
Άρα
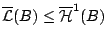 .
.
Δείξαμε ότι τα δύο εξωτερικά μέτρα
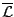 και
και
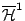 ταυτίζονται. Οπότε ο περιορισμός τους σε μετρήσιμα σύνολα (με την έννοια του Καραθεοδωρή)
ταυτίζεται επίσης.
ταυτίζονται. Οπότε ο περιορισμός τους σε μετρήσιμα σύνολα (με την έννοια του Καραθεοδωρή)
ταυτίζεται επίσης.

Πιο γενικά το δισδιάστατο μέτρο Hausdorff εκφράζει εμβαδό μιας λείας επιφάνειας
πολλαπλασιαζμένο με 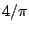 , ενώ το τριςδιάστατο μέτρο Hausdorff
εκφράζει τον όγκο ενός χώρου επί
, ενώ το τριςδιάστατο μέτρο Hausdorff
εκφράζει τον όγκο ενός χώρου επί 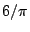 .
.
Υπάρχει μια σχέση που συνδέει το μέτρο Hausdorff με το μέτρο Lebesgue. Στο
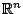 για
για 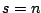 ισχύει
ισχύει
όπου 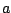 είναι μια σταθερά.
είναι μια σταθερά.





Next: Διάσταση Hausdorff
Up: Διάσταση Hausdorff
Previous: Διάσταση Hausdorff
Contents
Index
Khusainov Alexander
2002-10-25
![]() υποσυνόλων του
υποσυνόλων του ![]() , καλείται αριθμήσιμη κάλυψη του συνόλου
, καλείται αριθμήσιμη κάλυψη του συνόλου ![]() αν και μόνο αν
αν και μόνο αν
![]() μειώνεται, το
μειώνεται, το
![]() αυξάνεται. Τέλος
αυξάνεται. Τέλος ![]() σε μετρήσιμα
υποσύνολα του
σε μετρήσιμα
υποσύνολα του ![]() είναι s-διάστατο μέτρο
Hausdorff, και γράφεται
είναι s-διάστατο μέτρο
Hausdorff, και γράφεται
![]() .
.
![]() -διάστατου μέτρου
Hausdorff συναρτήσει του
-διάστατου μέτρου
Hausdorff συναρτήσει του ![]() . Βάσει του
επόμενου θεωρήματος μπορούμε να την ζωγραφίσουμε όπως στο σχήμα
3.1.
. Βάσει του
επόμενου θεωρήματος μπορούμε να την ζωγραφίσουμε όπως στο σχήμα
3.1.
![]() ,
αφού
,
αφού ![]() . Τότε έχουμε
. Τότε έχουμε
![]() . Είναι αντιληπτό ότι
το μηδέν-διάστατο μέτρο Hausdorff ενός συνόλου στην ουσία μας λέει από πόσα στοιχεία
αποτελείται το σύνολο.
. Είναι αντιληπτό ότι
το μηδέν-διάστατο μέτρο Hausdorff ενός συνόλου στην ουσία μας λέει από πόσα στοιχεία
αποτελείται το σύνολο.
![]() . Το μονο-διάστατο μέτρο Hausdorff ερμηνεύεται ως γενικευμένο
μέτρο που μετράει μήκος, οπως έχουμε πει και για το μέτρο Lebesgue στο
. Το μονο-διάστατο μέτρο Hausdorff ερμηνεύεται ως γενικευμένο
μέτρο που μετράει μήκος, οπως έχουμε πει και για το μέτρο Lebesgue στο ![]() .
Για τη ακρίβεια
.
Για τη ακρίβεια
![]() έχει πεπερασμένη διάμετρο
έχει πεπερασμένη διάμετρο ![]() , τότε
, τότε
![]() ,
άρα το
,
άρα το ![]() περιέχεται σ'' ένα κλειστό διαστημα
περιέχεται σ'' ένα κλειστό διαστημα ![]() μήκους
μήκους ![]() και ισχύει
και ισχύει
![]() . Από την σ-υποπροσθετικότητα του εξωτερικού μέτρου Lebesgue ,
έχουμε
. Από την σ-υποπροσθετικότητα του εξωτερικού μέτρου Lebesgue ,
έχουμε
![]() ,
αυτό ισχύει για όλες τις οικογένειες με σύνολα διαμέτρου μικρότερο από το
,
αυτό ισχύει για όλες τις οικογένειες με σύνολα διαμέτρου μικρότερο από το ![]() .
Από την μονοτονία του μέτρου έχουμε,
.
Από την μονοτονία του μέτρου έχουμε,
![]() και
και
![]() ταυτίζονται. Οπότε ο περιορισμός τους σε μετρήσιμα σύνολα (με την έννοια του Καραθεοδωρή)
ταυτίζεται επίσης.
ταυτίζονται. Οπότε ο περιορισμός τους σε μετρήσιμα σύνολα (με την έννοια του Καραθεοδωρή)
ταυτίζεται επίσης.
![]()
![]() , ενώ το τριςδιάστατο μέτρο Hausdorff
εκφράζει τον όγκο ενός χώρου επί
, ενώ το τριςδιάστατο μέτρο Hausdorff
εκφράζει τον όγκο ενός χώρου επί ![]() .
.
![]() για
για ![]() ισχύει
ισχύει