Τεχνική υπολογισμού της διάστασης Hausdorff

Για σχεδόν περισσότερα σύνολα η από πάνω εκτίμηση της διάστασης Hausdorff μπορεί να επιτευχθεί χρησιμοποιώντας την φυσική κάλυψη μικρών συνόλων.

Πρόταση 3.3.1   Υποθέτουμε ότι το σύνολο $F$ μπορεί να καλυφθεί από $n_k$ σύνολα διαμέτρου το πολύ $\delta_k$ με $\delta_k \rightarrow 0$ για $k\rightarrow \infty$. Τότε

$$\dim_{\mathcal{H}}F\leq \lim_{k\rightarrow \infty} - \frac{\log n_k}{\log \delta_k}$$

Επιπλέον, αν $n_k \delta_k^s$ παραμένει φραγμένο για $k\rightarrow \infty$, τότε $\mathcal{H}^s(F)<\infty$.

Απόδειξη: Από τον ορισμό του μέτρου Hausdorff έχουμε ότι

$$\mathcal{H}_{\delta_k}^s(F)\leq n_k\delta_k^s$$

Επιπλέον από τον ορισμό της διάστασης Hausdorff για να την υπολογίσουμε πρέπει να βρούμε τέτοιο $s$ για το οποίο $\mathcal{H}^s$ να είναι στο $(0,\infty)$. Άρα μπορούμε να θεωρήσουμε ότι $n_k\delta_k^s\geq 1$ (βασικά το $1$ μας βολεύει), οπότε $\log n_k +s \log \delta_k >0$ αν το $\delta$ είναι αρκετά μικρό (όριο για $k\rightarrow \infty$). Έχουμε

$$s\leq \lim -\frac{\log n_k}{\log \delta_k}$$

και $\dim_{\mathcal{H}}F\leq s$. Τέλος αν $n_k\delta_k$ φραγμένο τότε $\mathcal{H}_{\delta_k}^s(F)$ θα συγκλίνει σε πεπερασμένο όριο $\mathcal{Η}^s(F)$ για $k\rightarrow \infty$ $\Box$

Σχετικά συχνά η διάσταση που μας δίνει το ((εύκολο)) άνω φράγμα ισούται με την διάσταση Hausdorff ενός συνόλου. Όμως για να το δείξουμε αυτό, τις περισσότερες φορές, είναι δύσκολο. Για παράδειγμα, για να εκτιμήσουμε το άνω φράγμα αρκεί να υπολογίσουμε το άθροισμα τις μορφής $\sum_i (\mathop{\operator@font diam}U_i)^s$ για συγκεκριμένες καλύψεις $\{U_i\}$ του $F$, ενώ για το κάτω φράγμα πρέπει να δείξουμε ότι $\sum_i (\mathop{\operator@font diam}U_i)^s$ είναι μεγαλύτερο από μία θετική σταθερά για όλες τις $\delta$-καλύψεις του $F$.

Ένας τρόπος να προσπεράσουμε αυτές τις δυκολίες είναι να δείξουμε ότι κανένα ξεχωριστό σύνολο $U$ δεν μπορεί να καλύψει παραπάνω από το $F$ σε σχέση με το μέγεθος του ως $(\mathop{\operator@font diam}U)^s$. Τότε αν $\{U_i\}$ καλύπτει ολόκληρο το $F$ το άθροισμα $\sum_i (\mathop{\operator@font diam}U_i)^s$ δεν μπορεί να είναι πολύ μικρό.

Θεώρημα 3.3.1   Έστω $\overline{\mathcal{M}}$ πεπερασμένο εξωτερικό μέτρο στο $F$ και έστω για κάποιο $s$ υπάρχουν $c>0$ και $\delta>0$ τέτοια ώστε

$$\overline{\mathcal{M}}(U)\leq c(\mathop{\operator@font diam}U)^s$$ (3.5)

για όλα τα σύνολα $U$ με $\mathop{\operator@font diam}U\leq \delta$. Τότε $\mathcal{H}^s(F)\geq \overline{\mathcal{M}}(F)/c$ και

$$s\leq\dim_{\mathcal{H}}F$$

Απόδειξη: Αν $\{U_i\}$ είναι μια κάλυψη του $F$ τότε

$$0<\overline{\mathcal{M}}(F)=\overline{\mathcal{M}}(\bigcup_... ...hcal{M}}(U_i)\leq c\sum_i (\mathop{\operator@font diam}U_i)^s$$

παίρνοντας το κάτω πέρας έχουμε $\mathcal{H}_{\delta}^s(F)\geq \overline{\mathcal{M}}(F)/c$. Τέλος αν $\delta\rightarrow 0$ έχουμε $\mathcal{H}^s(F)\geq \overline{\mathcal{M}}(F)/c$. $\Box$

Παρατηρούμε πως το συμπέρασμα ότι $\mathcal{H}^s(F)\geq \mathcal{M}(F)/c$ παραμένει αληθές αν το πεπερασμένο εξωτερικό μέτρο $\overline{\mathcal{M}}$ είναι πεπερασμένο στο $\mathbb{R}^n$ και $F$ είναι υποσύνολο του $\mathbb{R}^n$.

Παράδειγμα: Το θεώρημα 3.3.1 δείνει μια γρήγορη εκτίμηση του κάτω φράγματος για το μέτρο Hausdorff του τριαδικού συνόλου Cantor, $C(1/3)$.

Έστω $\mathcal{M}$ το ((φυσικό)) πεπερασμένο μέτρο στο $C(1/3)$ έτσι ώστε κάθε ένα από τα $2^k$ ((βασικά)) διαστήματα μήκους $3^{-k}$ στο $C_k(1/3)$ της κατασκευής του τριαδικού συνόλου Cantor, να έχει $\mathcal{M}(I_{k,j})=2^{-k}$, $j=1,\ldots,2^k$. Έστω $U$ να είναι σύνολο με $\mathop{\operator@font diam}U<1$ και έστω $k$ να είναι ακέραιος τέτοιος ώστε $3^{-(k+1)}\leq \mathop{\operator@font diam}U <3^{-k}.$ Τότε $U$ τέμνει το πολύ ένα $I_{k,j}$, έτσι

$$\mathcal{M}(U)\leq 2^{-k}=(3^{-k})^{\frac{\log 2}{\log 3}}\leq (3 \mathop{\operator@font diam}U)^{\frac{\log 2}{\log 3}}$$

Άρα $\mathcal{Η}^{\log 2/\log 3}(C(1/3))>0$ και $\dim_\mathcal{H}C(1/3)\geq \log 2/\log 3$.

Figure: Το δεύτερο βήμα $k=2$ στην κατασκευή του συνόλου $C^1(1/3)=C(1/3)\times [0,1]$ και το παράδειγμα της κάλυψης. Κάθε ((κολώνα)) καλύπτεται από $3^k=9$ τετράγωνα μήκους πλευράς $3^{-k}=\frac{1}{9}$ και διαμέτρου $3^{-k}\sqrt{2}=\frac{\sqrt{2}}{9}$, συνολικά υπάρχουν $2^k=4$ ((κολώνες)).

Παράδειγμα: Έστω $C^1(1/3)=C(1/3)\times [0,1]\subset \mathbb{R}^2$ να είναι το γνόμενο του τριαδικού συνόλου Cantor, $C(1/3)$, με το κλειστό διάστημα $[0,1]$. Τότε $\dim_\mathcal{H} C^1(1/3)=1+\log 2/\log 3=s$ με $0<\mathcal{H}^s(C^1(1/3))<\infty$.
Απόδειξη: Για κάθε $k$, υπάρχει κάλυψη του $C(1/3)$ από $2^k$ διαστήματα μήκους $3^{-k}$. Μια σειρά από $3^k$ τετράγωνα μήκους πλευράς $3^{-k}$, δηλαδή διαμέτρου $3^{-k}\sqrt{2}$, καλύπτει το κομμάτι του $C^1(1/3)$ που είναι $I_{k,j}\times [0,1]$, άρα για να καλύψουμε όλο το $C^1(1/3)$ χρεαζόμαστε $2^k$ τέτοιες σειρές, δηλαδή το $C^1(1/3)$ μπορεί να καλυφθεί από $2^k 3^k$ τετράγωνα μήκους πλευράς $3^{-k}$, σχήμα 3.3.

Έτσι το πάνω όριο βρίσκουμε να είναι

$$\mathcal{H}^s_{3^{-k}\sqrt{2}}(C^1(1/3))\leq 3^k 2^k (3^{-k}\sqrt{2})^{1+\frac{\log 2}{\log 3}} =(\sqrt{2})^s$$

και

$$\begin{eqnarray*} \dim_{\mathcal{H}} C^1(1/3)&\leq& \lim_{k\rightarrow \infty}\... ...}}\\ &=& \frac{\log 3+\log 2}{\log 3}=1+\frac{\log 2}{\log 3} \end{eqnarray*}$$

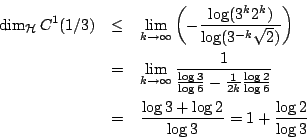
Ορίζουμε το πεπερασμένο μέτρο $\mathcal{M}$ στο $C^1(1/3)$ πέρνοντας το ((φυσικό)) πεπερασμένο μέτρο πάνω στο $C(1/3)$ όπως το έχουμε περιγράψει στο προηγούμενο παράδειγμα (δηλαδή κάθε διάστημα $I_{k,j}$ μήκους $3^{-k}$ έχει μέτρο $2^{-k}$) και κατανέμοντάς τα ομοιόμορφα πάνω στα ορθογώνια που δημιουργούνται από το γινόμενο του $I_{k,j}\times [0,1]$. Έτσι αν $U$ είναι ορθογώνιο με πλευρές παράλληλες προς άξωνες, ύψους $h$ και βάσης κάποιο $I_{k,j}$, τότε $\mathcal{M}(U)=h 2^{-k}$. Οποιοδήποτε σύνολο $U$ περιέχεται σε τετράγωνο πλευράς $\mathop{\operator@font diam}U$ με πλευρές παράλληλες στους άξωνες. Αν $3^{-(k+1)}\leq \mathop{\operator@font diam}U < 3^{-k}$, τότε $U$ τέμνει το πολύ μια λωρίδα $I_{k,j}\times [0,1]$, έτσι

$$\begin{eqnarray*} \mathcal{Μ}(U)\leq (\mathop{\operator@font diam}U)2^{-k} \leq... ...leq& 3^{\frac{\log 2}{\log 3}}(\mathop{\operator@font diam}U)^s \end{eqnarray*}$$

Από το θεώρημα 3.3.1 $\mathcal{H}^s(C^1(1/3))>0$, και $\dim_{\mathcal{H}}C^1(1/3)\geq 1+\log 2/\log3$. $\Box$

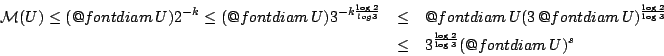
Παρατηρούμε ότι η διάσταση Hausdorff του γινομένου δύο συνόλων ισούται με το άθροισμα των διαστάσεων Hausdorff των συνόλων $\dim_{\mathcal{H}}C(1/3)\times [0,1] = \dim_{\mathcal{H}}C(1/3) +\dim_{\mathcal{H}}[0,1]$.

Παράδειγμα: Ο στόχος Cantor είναι ένα υποσύνολο του επιπέδου, ορισμένο σε πολικές συντεταγμένες με

$$C^{\circ}=\{(r,\vartheta)\ \hbox{όπου}\ r\in C(1/3) \ \hbox{και}\ 0\leq \vartheta \leq 2\pi \}$$

όπου $C(1/3)$ είναι το τριαδικό σύνολο Cantor, σχήμα 3.4. Τότε $\dim_{\mathcal{H}}C^{\circ}(1/3)= 1+\log 2/\log 3$
Απόδειξη: Έστω $f:\mathbb{R}^2\rightarrow \mathbb{R}^2$ είναι η $f(x,y)=(x\cos y,x\sin y)$. Η $f$ ικανοποιεί την συνθήκη Lipschitz και $C^{\circ}(1/3)=f[C(1/3)\times [0,2\pi ]]$

Έτσι από την πρόταση 3.2.1 και το προηγούμενο παράδειγμα έχουμε

$$\begin{eqnarray*} \dim_{\mathcal{H}}C^{\circ}(1/3)&\leq& \dim_{\mathcal{H}}(C(1... ...) + \dim_{\mathcal{H}}[0,2\pi]\\ &=& \frac{\log 2}{\log 3} +1 \end{eqnarray*}$$

Αν τώρα περιορίσουμε την $f$ στο $[2/3,1]\times[0,\pi]$ τότε η $f$ είναι bi-Lipschitz δηλαδή $c_1\vert x-y\vert\leq \vert f(x)-f(y)\vert\leq c_2\vert x-y\vert$ για κάποια σταθερά $c_1,c_2\in \mathbb{R}$. Όμως για bi-Lipschitz συναρτήσεις ισχύει ότι $\dim_{\mathcal{H}}f[A]=\dim_{\mathcal{H}}A$, αρκεί να εφαρμόσουμε την πρόταση 3.2.1 για την $f^{-1}:f[A]\rightarrow A$ για να πάρουμε την ανάποδη ανισότητα που χρειάζεται.

Οπότε αφού $f[(C(1/3)\cap [2/3,1])\times[0,\pi]]\subset C^{\circ}(1/3)$ έχουμε

$$\begin{eqnarray*} \dim_{\mathcal{H}}C^{\circ}(1/3)&\geq& \dim_{\mathcal{H}}f[(C... ...])) +\dim_{\mathcal{H}}[0,\pi]\\ &=& \frac{\log 2}{\log 3} +1 \end{eqnarray*}$$

$\Box$

Figure: Στόχος Cantor είναι το ίχνος που αφήνει το σύνολο Cantor $C(1/3)$ αν κάνει πλήρη περιστροφή γύρο από το σημείο $0$

Η επόμενη γενική κατασκευή ενός υποσυνόλου του $\mathbb{R}$ μπορεί να θεωρηθεί ως γενίκευση της κατασκευής του συνόλου Cantor. Έστω $[0,1]=E_0\supset E_1\supset E_2\supset\ldots$ είναι φθίνουσα ακολουθία συνόλων, με κάθε $E_k$ να είναι η ένωση πεπερασμένων ξένων κλειστών διαστημάτων, θα τα λέμε βασικά διαστήματα, με κάθε διάστημα του $E_k$ να περιέχει τουλάχιστον δύο διαστήματα του $E_{k+1}$ και το μέγιστο μήκος των διαστημάτων του $E_k$ να τείνει στο μηδέν, όταν $k\rightarrow \infty$. Τότε το σύνολο

$$F=\bigcap_{k=0}^{\infty} E_k$$

είναι παντού μη συνεκτικό υποσύνολο του $[0,1]$ που γενικά είναι κλασματικής διαστάσης.

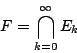
Τα πάνω φράγματα της διάστασης Hausdorff βγαίνουν εύκολα αν πάρουμε για καλύψεις τα διαστήματα του $E_k$, για κάθε $k$. Όσο για το κάτω φράγμα είναι πιο δύσκολο να το βρούμε.

Στα ακόλουθα παραδείγματα η πάνω εκτίμηση της δίαστασης Hausdorff εξαρτάται από τον αριθμό και το μέγεθος των βασικών διαστημάτων, ενώ η κάτω εκτίμηση εξαρτάται από τα κενά μεταξύ των βασικών διαστημάτων. Για να πετύχουμε την ισότητα (της πάνω και κάτω εκτίμησης), τα διαστήματα του $E_{k+1}$ θα πρέπει να είναι ((σχεδόν ομαλά κατανεμημένα)) μέσα στα διαστήματα του $E_k$.

Figure: Γενική κατασκευή του συνόλου Cantor

Παράδειγμα: Έστω $s\in (0,1)$. Υποθέτουμε ότι $E_k$ στην γενική κατασκευή έχει την παρακάτω ιδιότητα: Για κάθε βασικό διάστημα $I$ του $E_k$, τα διαστήματα $I_1,\ldots,I_m$ ($m\geq 2$) του $E_{k+1}$ που περιέχονται στο $I$ είναι ίσου μήκους και ισαπέχουν. Τα μήκη δίνονται από

$$(\mathop{\operator@font diam}I_i)^s=\frac{1}{m}(\mathop{\operator@font diam}I)^s\ \ ,1\leq i\leq n$$ (3.6)

με τα αριστερά άκρα του $I_1$ και $I$ να συμπίπτουν, όπως και τα δεξιά άκρα του $I_m$ και $I$. Τότε $\dim_{\mathcal{H}}F=s$ και $0<\mathcal{H}^s<\infty$. Προσοχή! το $m$ μπορεί να διαφέρει από βήμα σε βήμα, με αποτέλεσμα να έχουμε ποικιλία μηκών για τα βασικά διαστήματα του $E_k$.
Απόδειξη: Με $I$ και $I_i$ όπως παραπάνω έχουμε

$$(\mathop{\operator@font diam}I)^s=\sum_{i=1}^{m}(\mathop{\operator@font diam}I_i)^s$$ (3.7)

Εφαρμόζοντας αυτό επαγωγικά στα διαστήματα του $Ε_κ$ για ((καλά)) $k$ έχουμε ότι για κάθε $k$, $\sum (\mathop{\operator@font diam}I)^s$ όπου το άθροισμα είναι πάνω σε όλα τα βασικά διαστήματα του $E_k$. Τα διαστήματα του $E_k$ καλύπτουν το $F$, και αφού το διάστημα με μέγιστο μήκος τείνει στο μηδέν για $k\rightarrow \infty$, έχουμε ότι $\mathcal{H}_{\delta}^s(F)\leq 1$ και για $\delta$ αρκετά μικρό $\mathcal{H}^s(F)\leq 1$.

Τώρα κατανέμουμε το πεπερασμένο μέτρο $\mathcal{M}$ στο $F$ με τέτοιο τρόπο ώστε $\mathcal{Μ}(I) =(\mathop{\operator@font diam}I)^s$ όταν $I$ είναι βασικό διάστημα. Έτσι ξεκινώντας με $\mathcal{M}([0,1])=1$ το μοιράζουμε ίσα μεταξύ κάθε διαστήματος του $E_1$ στην συνέχεια το πεπερασμένο μέτρο σε κάθε ένα από αυτά τα δίαστήματα μοιράζεται ίσα μεταξύ κάθε υποδιαστήματος του $E_2$ κ.τ.λ.. Η ισότητα 3.7 εξασφαλίζει ότι έχουμε πεπερασμένο μέτρο στο $F$ με $\mathcal{M}(I)=(\mathop{\operator@font diam}I)^s$ για κάθε βασικό διάστημα. Εκτιμάμε το $\mathcal{M}(U)$ για οποιοδήποτε διάστημα $U$ με ακραία σημεία στο $F$. Έστω $I$ να είναι το μικρότερο βασικό διάστημα που περιέχει $U$, έστω $I$ είναι ένα διάστημα του $E_k$ και έστω $I_i,\dots,I_m$ είναι τα διαστημάτα του $E_{k+1}$ που περιέχονται στο $I$. Τοτε το $U$ τέμνει $j\geq 2$ από τα $I_i$, αλλιώς το $U$ θα περιεχόταν σε μικρότερο βασικό διάστημα. Τα κενά μεταξύ διαδοχικών $I_i$ είναι

$$\begin{eqnarray*} \frac{\mathop{\operator@font diam}I - m \mathop{\operator@fon... ...})}{m-1}\\ &\geq& c_s \frac{\mathop{\operator@font diam}I}{m} \end{eqnarray*}$$

χρησιμοποιώντας την 3.6, όπου $c_s=1-2^{1-1/s}$. Έτσι

$$\mathop{\operator@font diam}U \geq \frac{j-1}{m}c_s \mathop... ...ont diam}I\geq \frac{j}{2m} c_s \mathop{\operator@font diam}I$$

από την ισότητα 3.7

$$\begin{eqnarray*} \mathcal{M}(U)&\leq& j \mathcal{M}(I_i)=j(\mathop{\operator@f... ...U)^s \\ &\leq& 2^s c_s^{-s} (\mathop{\operator@font diam}U)^s \end{eqnarray*}$$

Αυτό ισχύει για κάθε διάστημα $U$ με ακριανά σημεία στο $F$ και άρα για κάθε $U$. Από το θεώρημα 3.3.1 έχουμε $\mathcal{H}^s(F)>0$ και $\dim_{\mathcal{H}}F\geq s$ $\Box$

Όταν το $m$ παραμένει σταθερό κατά την διάρκια της κατασκευής του παραπάνω παραδείγματος, τα σύνολα τα καλούμε ομοιόμορφα σύνολα Cantor .

Figure: Ομοιόμορφο σύνολο Cantor με $m=3$ και $\lambda=\frac{4}{15}$. $\dim_{\mathcal{H}}F=\frac{\ln 3}{\ln 15/4}$

Παράδειγμα: Έστω $m\geq 2$ σταθερό και $0<\lambda<1/m$. Έστω $F$ είναι το σύνολο που παίρνουμε από την κατασκευή στην οποία κάθε βασικό διάστημα $I$ ανικαθιστάται από ισαπέχοντα υποδιαστήματα μήκους $\lambda \mathop{\operator@font diam}I$ και τα άκρα του $I$ συμπίπτουν με τα άκρα των ακραίων υποδιαστημάτων. Τότε $\dim_{\mathcal{H}}F=- \log m/\log \lambda$ και $0<\mathcal{H}^{-\log m/\log \lambda}(F)) <\infty$
Απόδειξη: Το σύνολο $F$ παράγεται παίρνοντας $m$ σταθερό, και έστω $s=-\log m /\log \lambda$. Τότε από προηγούμενο παράδειγμα η εξίσωση 3.6 γίνεται $(\lambda \mathop{\operator@font diam}I)^s=(\mathop{\operator@font diam}I)^s/m$ κάτι που ισχύει για συγκεκριμένο $s$, άρα $\dim_{\mathcal{H}}F=s$ $\Box$

Παρόλο που το θεώρημα 3.3.1 βασίζεται σε απλή ιδέα είδαμε πόσο πολύ χρήσιμο μπορεί να είναι στην εύρεση της διάστσης Hausdorff .