




Next: Κατασκευή Εξωτερικού Μέτρου
Up: Μέτρο
Previous: Μέτρο Lebesgue
Contents
Index
Ορισμός 2.2.6
Έστω
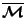 εξωτερικό μέτρο στο
εξωτερικό μέτρο στο  . Ένα υποσύνολο
. Ένα υποσύνολο
 του
του  θα καλείται
θα καλείται
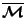 -μετρήσιμο σύνολο (με την έννοια
του Καραθεοδώρη) αν και μόνο αν
-μετρήσιμο σύνολο (με την έννοια
του Καραθεοδώρη) αν και μόνο αν
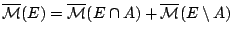 για όλα τα υποσύνολα
για όλα τα υποσύνολα 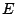 του
του  .
.
Θεώρημα 2.2.4
Έστω
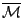 εξωτερικό μέτρο στο
εξωτερικό μέτρο στο  και
και
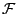 μια συλλογή
μια συλλογή
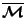 -μετρήσιμων
υποσυνόλων του
-μετρήσιμων
υποσυνόλων του  . Τότε η
. Τότε η 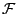 είναι σ-άλγεβρα στο
είναι σ-άλγεβρα στο  και το
και το
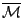 είναι σ-προσθετική στο
είναι σ-προσθετική στο
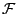 .
.
Απόδειξη: Αρχικά θα δείξουμε πως 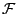 είναι σ-άλγεβρα. Θα δείξουμε
πρώτα ότι είναι άλγεβρα και μετά χρησιμοποιώντας την πρόταση 2.1.1
δείχνουμε ότι είναι σ-άλγεβρα. Σύμφωνα με
τον ορισμό 2.1.2
πρέπει το κενό και το ίδιο το σύνολο
είναι σ-άλγεβρα. Θα δείξουμε
πρώτα ότι είναι άλγεβρα και μετά χρησιμοποιώντας την πρόταση 2.1.1
δείχνουμε ότι είναι σ-άλγεβρα. Σύμφωνα με
τον ορισμό 2.1.2
πρέπει το κενό και το ίδιο το σύνολο  να ανήκουν στην
να ανήκουν στην
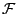 το οποίο ισχύει αφού
το οποίο ισχύει αφού
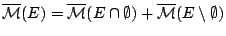 και
και
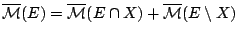 αληθεύουν (
αληθεύουν (
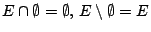 και
και
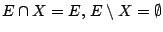 και
και
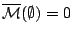 ).
).
Επίσης εάν
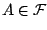 τότε και
τότε και
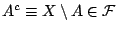 αφού
αφού
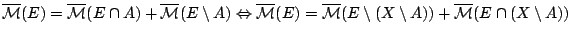 .
.
Έμεινε να δείξουμε ότι η 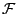 είναι κλειστή ως προς πεπερασμένες
τομές ή ενώσεις. Έστω
είναι κλειστή ως προς πεπερασμένες
τομές ή ενώσεις. Έστω
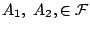 τότε εξ''
υποθέσεως ξέρουμε ότι για οποιοδήποτε υποσύνολο
τότε εξ''
υποθέσεως ξέρουμε ότι για οποιοδήποτε υποσύνολο 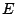 του
του  ισχύει
ισχύει
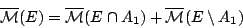 |
(2.6) |
Αφού
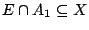 ισχύει και
ισχύει και
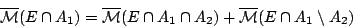 |
(2.7) |
Απο 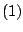 και
και 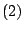 έχουμε
έχουμε
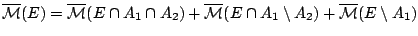 .
.
Ο σκοπός μας, σαν πρωτο στάδιο, είναι να δείξουμε ότι
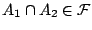 δηλαδή να καταλήξουμε στην σχέση
δηλαδή να καταλήξουμε στην σχέση
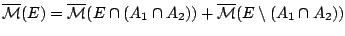 το πρώτο
μέρος του αθροίσματος το έχουμε, αρκεί να δείξουμε ότι
το πρώτο
μέρος του αθροίσματος το έχουμε, αρκεί να δείξουμε ότι
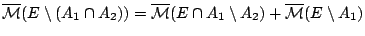 κάτι που ισχύει αφού
κάτι που ισχύει αφού
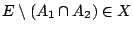 και
και
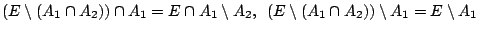 .
.
Τώρα επαγωγικά έχουμε για πεπερασμένες τομές ότι η 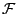 είναι
κλειστή, άρα η
είναι
κλειστή, άρα η 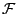 είναι άλγεβρα.
είναι άλγεβρα.
Είναι εύκολο να δούμε ότι για
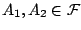 και
και
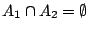 έχουμε ότι
έχουμε ότι
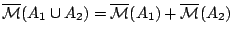 αφού
αφού
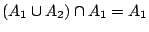 και
και
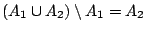
Επαγωγικά ισχύει για πεπερασμένες ενώσεις

Έστω τώρα 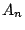 ακολουθία ξένων ανά δυο μεταξύ τους συνόλων της
ακολουθία ξένων ανά δυο μεταξύ τους συνόλων της
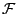 και
και
 . Αν δείξω ότι
. Αν δείξω ότι
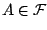 τότε σύμφωνα με την πρόταση 2.1.1
η
τότε σύμφωνα με την πρόταση 2.1.1
η 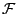 είναι σ-άλγεβρα.
είναι σ-άλγεβρα.
Έχουμε δείξει ότι η 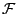 είναι άλγεβρα, άρα αν πάρουμε
από την
είναι άλγεβρα, άρα αν πάρουμε
από την 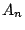 πεπερασμένα στοιχεία, έστω
πεπερασμένα στοιχεία, έστω
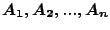 τότε η
τομή τους όπως και η ένωση θα ανήκει στην
τότε η
τομή τους όπως και η ένωση θα ανήκει στην 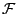 αρα (για
την ένωση), ισχύει πως για κάθε
αρα (για
την ένωση), ισχύει πως για κάθε 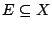 έχουμε
έχουμε
Τα στοιχεία της ακολουθίας
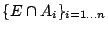 είναι και αυτά
ξένα μεταξύ τους, οπότε ισχύει
είναι και αυτά
ξένα μεταξύ τους, οπότε ισχύει
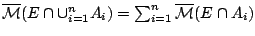 και αφού ισχύει
και αφού ισχύει
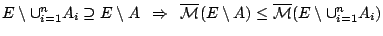 από
το ορισμό του εξωτερικού μέτρου --ιδιότητα (2)--, έχουμε
από
το ορισμό του εξωτερικού μέτρου --ιδιότητα (2)--, έχουμε
τώρα για
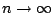 και επειδή το εξωτερικό μέτρο είναι
υποπροσθετικό έχουμε
και επειδή το εξωτερικό μέτρο είναι
υποπροσθετικό έχουμε
Τώρα, ξανά επιδή το εξωτερικό μέτρο είναι υποπροσθετικό έχουμε
Όμως
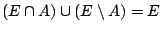 . Άρα
. Άρα
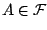 όποτε και η
όποτε και η 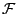 είναι σ-άλγεβρα και
επιπλέον έχουμε πως
είναι σ-άλγεβρα και
επιπλέον έχουμε πως
Αν όμως 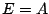 τότε
τότε
Δηλαδή η
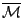 είναι σ-προσθετική στο
είναι σ-προσθετική στο
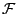 .
.

Θα γράφουμε σκέτο 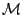 για τον περιορισμό του εξωτερικού
μέτρου
για τον περιορισμό του εξωτερικού
μέτρου
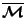 στην σ-άλγεβρα
στην σ-άλγεβρα 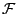 των
μετρήσιμων συνόλων, αφού τότε γίνεται μέτρο στην
των
μετρήσιμων συνόλων, αφού τότε γίνεται μέτρο στην 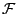 .
Έτσι βλέπουμε έναν τρόπο κατασκεύης μέτρου από ένα εξωτερίκο
μέτρο.
.
Έτσι βλέπουμε έναν τρόπο κατασκεύης μέτρου από ένα εξωτερίκο
μέτρο.
Πρόταση 2.2.9
Τα Lebesgue μετρήσιμα σύνολα είναι μετρήσιμα (με την έννοια του Καραθεοδωρή) ή αλλιώς, ένα υποσύνολο
 του
του  είναι Lebesgue μετρήσιμο αν και μόνο αν ισχύει
είναι Lebesgue μετρήσιμο αν και μόνο αν ισχύει
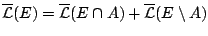 για όλα τα
για όλα τα
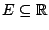
Απόδειξη: Έστω  είναι Lebesgue μετρήσιμο υποσύνολο του
είναι Lebesgue μετρήσιμο υποσύνολο του  και έστω
και έστω 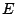 οποιοδήποτε υποσύνολο
του
οποιοδήποτε υποσύνολο
του
 , τότε η ανισότητα
, τότε η ανισότητα
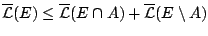 ισχύει λόγο της σ-υποπροσθετικότητας του εξωτερικού μέτρου. Έστω
ισχύει λόγο της σ-υποπροσθετικότητας του εξωτερικού μέτρου. Έστω
 τότε υπάρχει
ανοιχτό σύνολο
τότε υπάρχει
ανοιχτό σύνολο 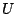 και κλειστό
και κλειστό 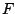 ώστε
ώστε
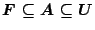 και
και
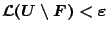 (από το θεώρημα 2.2.2). Έστω
(από το θεώρημα 2.2.2). Έστω 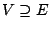 ανοιχτό σύνολο,
τότε
ανοιχτό σύνολο,
τότε
πέρνοντας το κάτω πέρας για όλα τέτοια 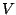 έχουμε
έχουμε
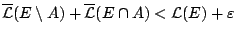 και αφού ισχύει για κάθε
και αφού ισχύει για κάθε 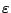 θετικό έχουμε τελικά
θετικό έχουμε τελικά
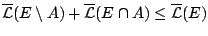
Αντίστροφα, έστω  είναι μετρήσιμο σύνολο (με την έννοια του Καραθεοδωρή). Θέωρουμε την περηπτώση όταν
είναι μετρήσιμο σύνολο (με την έννοια του Καραθεοδωρή). Θέωρουμε την περηπτώση όταν
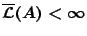 . Έστω
. Έστω
 και
και 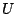 Lebesgue μετρήσιμο υπερσύνολο του
Lebesgue μετρήσιμο υπερσύνολο του  ώστε να ισχύει
ώστε να ισχύει
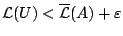 . Τώρα από υπόθεση έχουμε ότι
. Τώρα από υπόθεση έχουμε ότι
έτσι ώστε
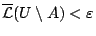 . Άρα υπάρχει ένα ανοιχτο σύνολο
. Άρα υπάρχει ένα ανοιχτο σύνολο
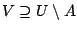 με
με
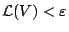 . Τότε
. Τότε 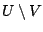 είναι Lebesgue μετρήσιμο και
είναι Lebesgue μετρήσιμο και
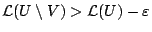 , έτσι υπάρχει κλειστό σύνολο
, έτσι υπάρχει κλειστό σύνολο
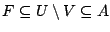 με
με
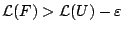 . Έτσι
. Έτσι
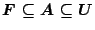 και
και
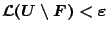 . Άρα το
. Άρα το  είναι Lebesgue μετρήσιμο.
είναι Lebesgue μετρήσιμο.

Στην επόμενη παράγραφο θα παρουσιάσουμε δύο τρόπους κατασκευής εξωτερικού μέτρου.





Next: Κατασκευή Εξωτερικού Μέτρου
Up: Μέτρο
Previous: Μέτρο Lebesgue
Contents
Index
Khusainov Alexander
2002-10-25
![]() τότε και
τότε και
![]() αφού
αφού
![]() .
.
![]() είναι κλειστή ως προς πεπερασμένες
τομές ή ενώσεις. Έστω
είναι κλειστή ως προς πεπερασμένες
τομές ή ενώσεις. Έστω
![]() τότε εξ''
υποθέσεως ξέρουμε ότι για οποιοδήποτε υποσύνολο
τότε εξ''
υποθέσεως ξέρουμε ότι για οποιοδήποτε υποσύνολο ![]() του
του ![]() ισχύει
ισχύει
![]() δηλαδή να καταλήξουμε στην σχέση
δηλαδή να καταλήξουμε στην σχέση
![]() το πρώτο
μέρος του αθροίσματος το έχουμε, αρκεί να δείξουμε ότι
το πρώτο
μέρος του αθροίσματος το έχουμε, αρκεί να δείξουμε ότι
![]() κάτι που ισχύει αφού
κάτι που ισχύει αφού
![]() και
και
![]() .
.
![]() είναι
κλειστή, άρα η
είναι
κλειστή, άρα η ![]() είναι άλγεβρα.
είναι άλγεβρα.
![]() και
και
![]() έχουμε ότι
έχουμε ότι
![]() αφού
αφού
![]() και
και
![]()
![]()
![]() ακολουθία ξένων ανά δυο μεταξύ τους συνόλων της
ακολουθία ξένων ανά δυο μεταξύ τους συνόλων της
![]() και
και
![]() . Αν δείξω ότι
. Αν δείξω ότι
![]() τότε σύμφωνα με την πρόταση 2.1.1
η
τότε σύμφωνα με την πρόταση 2.1.1
η ![]() είναι σ-άλγεβρα.
είναι σ-άλγεβρα.
![]() είναι άλγεβρα, άρα αν πάρουμε
από την
είναι άλγεβρα, άρα αν πάρουμε
από την ![]() πεπερασμένα στοιχεία, έστω
πεπερασμένα στοιχεία, έστω
![]() τότε η
τομή τους όπως και η ένωση θα ανήκει στην
τότε η
τομή τους όπως και η ένωση θα ανήκει στην ![]() αρα (για
την ένωση), ισχύει πως για κάθε
αρα (για
την ένωση), ισχύει πως για κάθε ![]() έχουμε
έχουμε
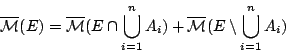
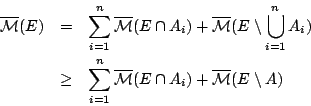
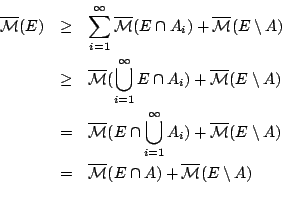
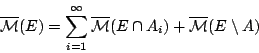
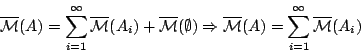
![]() για τον περιορισμό του εξωτερικού
μέτρου
για τον περιορισμό του εξωτερικού
μέτρου
![]() στην σ-άλγεβρα
στην σ-άλγεβρα ![]() των
μετρήσιμων συνόλων, αφού τότε γίνεται μέτρο στην
των
μετρήσιμων συνόλων, αφού τότε γίνεται μέτρο στην ![]() .
Έτσι βλέπουμε έναν τρόπο κατασκεύης μέτρου από ένα εξωτερίκο
μέτρο.
.
Έτσι βλέπουμε έναν τρόπο κατασκεύης μέτρου από ένα εξωτερίκο
μέτρο.
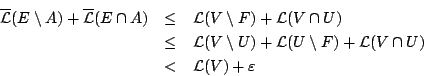
![]() είναι μετρήσιμο σύνολο (με την έννοια του Καραθεοδωρή). Θέωρουμε την περηπτώση όταν
είναι μετρήσιμο σύνολο (με την έννοια του Καραθεοδωρή). Θέωρουμε την περηπτώση όταν
![]() . Έστω
. Έστω
![]() και
και ![]() Lebesgue μετρήσιμο υπερσύνολο του
Lebesgue μετρήσιμο υπερσύνολο του ![]() ώστε να ισχύει
ώστε να ισχύει
![]() . Τώρα από υπόθεση έχουμε ότι
. Τώρα από υπόθεση έχουμε ότι