Μέτρο

Η έννοια του μέτρου έρχεται όταν χρειάζεται να συγκρίνουμε τα σύνολα. Ξέρουμε να μετράμε διαστήματα μέσα στο $\mathbb{R}$, πχ το διάστημα $[a,b]$ έχει μέτρο (μήκος) $b-a$. Το θέμα είναι τι γίνεται όταν τα σύνολά μας δεν είναι διαστήματα, ούτε ένωση διαστημάτων και πιο γενικά ούτε καν ανήκουν στα συμβατικά σύνολα που χρησιμοποιούμε, όπως $\mathbb{R}$, $\mathbb{R}^2$, κτλ (π.χ. σύνολο ανθρώπων).

Θα ορίσουμε μια κλάση συναρτήσεων που κάθε μια θα αποκαλούμε μέτρο, οι οποίες θα παίρνουν ένα σύνολο και θα το αντιστοιχούν σε έναν μη αρνητικό πραγματικό αριθμό. Θα προσπαθήσουμε να βάλουμε και κάποιους περιορισμούς έτσι ώστε το αποτέλεσμα που θα μας δίνει το μέτρο να παρουσιάζει ενδιαφέρον, δηλαδή να εκφράζει κάποιο είδος (τρόπο) σύγκρισης.

Ορισμός 2.2.1   Έστω $X$ σύνολο και $\mathcal{A}$ σ-άλγεβρα στο $X$. Μια συνολοσυνάρτηση $\mathcal{M}:\mathcal{A}\rightarrow [0,\infty]$ λέγεται μέτρο αν ικανοποιεί τις ιδιότητες:

1. $\mathcal{M}(\emptyset)=0$,
2. Για οποιαδήποτε ακολουθία $A_n\in\mathcal{A}$ ξένων ανά δύο στοιχείων να ισχύει
   
   $$\mathcal{M}\left(\bigcup_{n\in\mathbb{N}}A_n\right)=\sum^{\infty}_{n=1} \mathcal{M}(A_n)$$
   
   

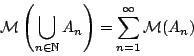
Η ιδιότητα (2) λέγεται αριθμήσιμη προσθετικότητα ή σ-προσθετικότητα. Θα παρουσιάσουμε στην συνέχεια κάποιες χρήσιμες ιδιότητες του μέτρου.

Πρόταση 2.2.1   Έστω $X$ σύνολο, $\mathcal{A}$ σ-άλγεβρα σ'' αυτό και $\mathcal{M}$ μέτρο που ορίζεται στην $\mathcal{A}$. Αν $A,B\in\mathcal{A}$ και $A\subset B$ τότε $\mathcal{M}(A)\leq\mathcal{M}(B)$. Αν επιπλέον $\mathcal{M}(A)<\infty$ τότε $\mathcal{M}(B\setminus A)=\mathcal{M}(B)-\mathcal{M}(A)$

Απόδειξη: Έχουμε $A\subset B$ τότε όμως $A$ και $B\setminus A$ είναι ξένα μεταξύ τους και $B\setminus A=B\cap A^c\in\mathcal{A}$ (αφού $\mathcal{A}$ είναι σ-άλγεβρα). Από την στιγμή που το μέτρο $\mathcal{M}$ είναι σ-προσθετικό ισχύει $\mathcal{M}(B)= \mathcal{M}(A\cup (B\setminus A))=\mathcal{M}(A)+\mathcal{M}(B\setminus A)$ (και αφού το μέτρο είναι μη αρνητική συνάρτηση εχούμε δηλαδή $\mathcal{M}(B\setminus A)\geq 0$) $\Rightarrow \mathcal{M}(B)\geq\mathcal{M}(A)$.

Για την δεύτερη σχέση απαιτούμε το μέτρο του $Α$ να είναι πεπερασμένο γιατί αλλιώς δεν έχει νόημα η ζητούμενη ισότητα. $\Box$

Η παραπάνω πρόταση μας λέει πως το μέτρο $\mathcal{M}$ είναι μονότονη συνάρτηση.

Παράδειγμα: Έστω $X$ σύνολο, $\mathcal{P}(X)$ δυναμοσύνολο του $X$, $x$ ένα στοιχείο του $X$ και η συνάρτηση $\mathcal{M}_x:\mathcal{P}(X)\rightarrow \mathbb{R}$

$$\mathcal{M}_x(A)=\left\{ \begin{array}{cc} 0 \ \hbox{αν... ... A \end{array} \right. \ \hbox{για κάθε}\ A\in\mathcal{A}$$

To $\mathcal{M}_x$ είναι μέτρο. Αυτό γιατί το δυναμοσύνολο του Χ είναι σ-άλγεβρα και ισχύει $\mathcal{M}_x(\emptyset)=0$ αφού $x\notin\emptyset$ και επιπλέον αν έχουμε $A_1,A_2,...\subseteq X$ (όποτε ανήκουν και στο δυναμοσύνολο του Χ) ξένα ανά δυο μεταξύ τους και $x$ ανήκει σε ένα από αυτά (ακριβώς σ'ένα γιατί είναι ξένα μεταξύ τους) ή δεν ανήκει σε κανένα, τότε το $x$ θα ανήκει ή δεν θα ανήκει στην $\cup_{n\in\mathbb{N}}A_n$ αντίστοιχα. Άρα αν $x$ δεν ανήκει σε κανένα τότε $\mathcal{M}_x\left(\cup_{n\in\mathbb{N}}A_n\right)=\sum^{\infty}_{n=1}\mathcal{M}_x(A_n)=0$ αλλιώς $\mathcal{M}_x\left(\cup_{n\in\mathbb{N}}A_n\right)=\sum^{\infty}_{n=1}\mathcal{M}_x(A_n)=1$

To $\mathcal{M}_x$ καλείται μοναδιαίο μέτρο συγκεντρωμένο στο $x$ ή μέτρο Dirac στο σημείο $x$.

Παράδειγμα: Έστω $\mathbb{N}$ σύνολο φυσικών αριθμών και $\mathcal{P}(\mathbb{N})$ δυναμοσύνολο του $\mathbb{N}$. Ορίζουμε την συνολοσυνάρτηση $\mathcal{M}:\mathcal{P}\rightarrow [0,+\infty]$ να είναι το πλήθος των στοιχείων του $A$ αν το $Α$ εχει πεπερασμένα στοιχεία και $\infty$ αν το $Α$ έχει άπειρα στοιχεία για κάθε $A\in\mathcal{P}$. Είναι εύκολο να δει κανείς πως η συνάρτηση $\mathcal{M}$ είναι μέτρο.

Τα μέτρα που παρουσιάσαμε στα παράδειγματα είναι σχετικά απλά. Για να κατασκευάσουμε πιο πολύπλοκα και γενικά πιο ενδιαφέροντα μέτρα θα χρειαστεί μια μέθοδος κατασκευής τους. Για το λόγο αυτό εισάγουμε την έννοια του εξωτερικού μέτρου το οποίο όπως θα δούμε παρακάτω, υπό κατάλληλες συνθήκες μπορεί να γίνει μέτρο.

Το εξωτερικό μέτρο θα είναι μια μη-αρνητική, μονοτονική και σ-υποπροσθετική συνολοσυνάρτηση που στέλνει το κενό σύνολο στο μηδέν.

Ορισμός 2.2.2   Έστω $X$ ένα σύνολο και $\mathcal{P}(X)$ το δυναμόσυνολο του. Μια συνολοσυνάρτηση $\mathcal{\overline{M}}:\mathcal{P}(X)\rightarrow [0,\infty]$ λέγεται εξωτερικό μέτρο στο $X$ αν ικανοποιεί τις ιδιότητες

1. $\mathcal{\overline{M}}(\emptyset)=0$
2. αν $A\subseteq B\subseteq X$, τότε $\mathcal{\overline{M}}(A)\leq \mathcal{\overline{M}}(B)$
3. Για οποιαδήποτε ακολουθία $A_n\in X$ ισχύει
   
   $$\mathcal{\overline{M}}\left(\bigcup_{n\in\mathbb{N}}A_n\right)\leq \sum_{n=1}^{\infty}\mathcal{\overline{M}}(A_n)$$
   
   

Η ιδιότητα (3) λέγεται αριθμήσιμη υποπροσθετικότητα ή σ-υποπροσθετικότητα.

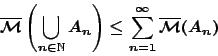
Η διαφορά λοιπόν του εξωτερικού μέτρου από το μέτρο είναι, πρώτον το εξωτερικό μέτρο δεν είναι κατ'' ανάγκη σ-προσθετικό και δεύτερον το εξωτερικό μέτρο ορίζεται στην μεγίστη σ-άλγεβρα (δυναμοσύνολο) του συνόλου και όχι σε οποιαδήποτε όπως το μέτρο.

Θα δώσουμε μια πρώτη γεύση του πως χρησιμοποιούμε το εξωτερικό μέτρο. Ο τρόπος σκέψης στην κατασκευή του μέτρου Lebesgue είναι παρόμοιος με την γενική μέθοδο κατασκευής που θα χρησημοποιήσουμε για να ορίσουμε το μέτρο Hausdorff.