Μια χρήσιμη γενίκευση της ιδέας του μήκους ενός υποσυνόλου του ![]() είναι μέτρο
Lebesgue του συνόλου.
είναι μέτρο
Lebesgue του συνόλου.
Δηλαδή το εξωτερικό μέτρο Lebesgue ενός συνόλου
Μπορούμε να τροποποιήσουμε λίγο τον ορισμό του εξωτερικού μέτρου Lebesgue, παίρνοντας το κάτω πέρας πάνω σε σύνολο αθροισμάτων των ημιανοιχτών διαστημάτων που το μήκος τους είναι μικρότερο από ένα θετικό αριθμό.
Απόδειξη: Κάθε διάστημα
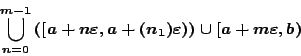
Θα δείξουμε τώρα ότι το εξωτερικό μέτρο Lebesgue που μόλις ορίσαμε είναι όντως εξωτερικό μέτρο.
Απόδειξη: Βάσει του ορισμού 2.2.3 ήδη ισχύει πως το
Έστω
![]() και
και ![]() ώστε
ώστε
![]() τότε
τότε
![]() άρα
άρα
![]() για
κάθε
για
κάθε
![]() άρα
άρα
![]() .
.
Έστω
![]() τότε κάθε κάλυψη του
τότε κάθε κάλυψη του ![]() είναι και κάλυψη του
είναι και κάλυψη του ![]() , το αντίστροφο δεν ισχύει. Άρα
το σύνολο
, το αντίστροφο δεν ισχύει. Άρα
το σύνολο
![]() είναι υποσύνολο
του αντίστοιχου συνόλου
είναι υποσύνολο
του αντίστοιχου συνόλου ![]() . Όμως αν
. Όμως αν
![]() τότε
τότε
![]() δηλαδή
δηλαδή
![]()
Έστω
![]() πρέπει να δείξουμε ότι το
πρέπει να δείξουμε ότι το
![]() είναι σ-υποπροσθετικό δηλαδή
είναι σ-υποπροσθετικό δηλαδή

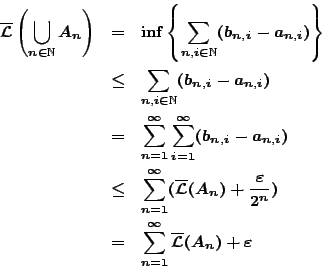
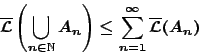
Έχοντας ορίσει το
![]() δεν σημαίνει ότι παρουσιάζει κάποιο ενδιαφέρον. Θα δείξουμε στην παρακάτω πρόταση
ότι το εξωτερικό μέτρο Lebesgue στέλνει τα διαστήματα του
δεν σημαίνει ότι παρουσιάζει κάποιο ενδιαφέρον. Θα δείξουμε στην παρακάτω πρόταση
ότι το εξωτερικό μέτρο Lebesgue στέλνει τα διαστήματα του ![]() στο μήκος τους.
στο μήκος τους.
Έστω τώρα
![]() και
και
![]() , θέτω
, θέτω
![]() τότε
τότε
![]() όμως
όμως ![]() είναι κλειστό και φραγμένο υποσύνολο του
είναι κλειστό και φραγμένο υποσύνολο του ![]() άρα από θέωρημα
1.5.5 είναι συμπαγές και από τον ορισμό 1.5.4 της συμπάγειας υπάρχει
άρα από θέωρημα
1.5.5 είναι συμπαγές και από τον ορισμό 1.5.4 της συμπάγειας υπάρχει
![]() ώστε
ώστε
![]() .
.
Ισχυρίζομαι ότι ισχύει
Για ![]() έχουμε
έχουμε
![]() οπότε
οπότε ![]() άρα
άρα ![]() . Έστω τώρα πως ισχύει για
. Έστω τώρα πως ισχύει για ![]() ,
δηλαδή αν
,
δηλαδή αν
![]() τότε
τότε
![]() .
Πρέπει να δείξω ότι ισχύει για
.
Πρέπει να δείξω ότι ισχύει για ![]() . Έστω λοιπόν
. Έστω λοιπόν
![]() τότε αν κάποιο
από τα διαστήματα
τότε αν κάποιο
από τα διαστήματα ![]() είναι ξένο με το
είναι ξένο με το ![]() μπόρει να παραλειφθεί από την κάλυψη, θα έχουμε όμως τότε
μπόρει να παραλειφθεί από την κάλυψη, θα έχουμε όμως τότε
![]() διαστήματα, για
διαστήματα, για ![]() διαστήματα έχουμε υποθέσει ότι ισχύει η ανισότητα 2.2. Μπορούμε επομένως να υποθέσουμε
πως
διαστήματα έχουμε υποθέσει ότι ισχύει η ανισότητα 2.2. Μπορούμε επομένως να υποθέσουμε
πως
![]() για όλα τα
για όλα τα ![]() . Από όλα τα
. Από όλα τα ![]() θα υπάρχει το μικρότερο. Χωρίς βλάβη
της γενικότητας το μετονομάζουμε σε
θα υπάρχει το μικρότερο. Χωρίς βλάβη
της γενικότητας το μετονομάζουμε σε ![]() τότε και αφού το
τότε και αφού το ![]() καλύπτεται, ισχύει
καλύπτεται, ισχύει ![]() , αν παράλληλα ισχύει πως
, αν παράλληλα ισχύει πως
![]() τότε
τότε
![]() όποτε δείξαμε την ανισότητα 2.2. Υποθέτουμε λοιπόν
όποτε δείξαμε την ανισότητα 2.2. Υποθέτουμε λοιπόν
![]() . Αφού
. Αφού ![]() τέμνει το
τέμνει το ![]() έχουμε
έχουμε ![]() , άρα
, άρα ![]() . Τουλάχιστον ένα από τα διαστήματα
. Τουλάχιστον ένα από τα διαστήματα
![]() , έστω
, έστω ![]() , καλύπτει το
, καλύπτει το ![]() . Ενώνοντας
. Ενώνοντας
![]() παίρνουμε κάλυψη με
παίρνουμε κάλυψη με ![]() διαστήματα.
Υποθέσαμε προηγουμένως ότι για
διαστήματα.
Υποθέσαμε προηγουμένως ότι για ![]() διαστήματα η ανισότητα 2.2 ισχύει, άρα από μαθηματική επαγωγή ισχύει η
ανισότητα 2.2.
διαστήματα η ανισότητα 2.2 ισχύει, άρα από μαθηματική επαγωγή ισχύει η
ανισότητα 2.2.
Αφού ισχύει η ανισότητα 2.2, ισχύει και
![]() . Οπότε έχουμε
. Οπότε έχουμε
![]() , αυτό ισχύει για κάθε
, αυτό ισχύει για κάθε
![]() άρα έχουμε
άρα έχουμε
![]() δηλαδή
δηλαδή
Στην συνέχεια θα υπολογίσουμε το ανοιχτό διάστημα ![]() . Έχουμε δείξει στην πρόταση 2.2.2 ότι
. Έχουμε δείξει στην πρόταση 2.2.2 ότι
![]() είναι εξωτερικό μέτρο άρα ισχύει η ιδιότητα (2) του ορισμού 2.2.2 του
εξωτερικού μέτρου. Τώρα έχουμε πως
είναι εξωτερικό μέτρο άρα ισχύει η ιδιότητα (2) του ορισμού 2.2.2 του
εξωτερικού μέτρου. Τώρα έχουμε πως
![]() . Αρκεί να δείξουμε ότι
. Αρκεί να δείξουμε ότι
![]() . Για
. Για
![]() ισχύει
ισχύει
![]() ,
το
,
το ![]() είναι όσο μικρό θέλουμε άρα
είναι όσο μικρό θέλουμε άρα
![]() . Δηλαδή
. Δηλαδή
![]() .
.
Τώρα
![]() . Ακριβώς για το ίδιο
λόγο ισχύει
. Ακριβώς για το ίδιο
λόγο ισχύει
![]() .
.
Τέλος αν έχουμε ![]() μη φραγμένο διάστημα τότε περιέχει
μη φραγμένο διάστημα τότε περιέχει ![]() με οσοδήποτε μεγάλο μήκος. Από την ιδιότητα
(2) του ορισμού 2.2.2 του εξωτερικού μέτρου έπεται
με οσοδήποτε μεγάλο μήκος. Από την ιδιότητα
(2) του ορισμού 2.2.2 του εξωτερικού μέτρου έπεται
![]() .
.
![]()
Άμεσα μπορούμε να ισχυριστούμε ότι κάθε φραγμένο υποσύνολο του ![]() έχει πεπερασμένο εξωτερικό
μέτρο Lebesgue. Αφού κάθε φραγμένο υποσύνολο
έχει πεπερασμένο εξωτερικό
μέτρο Lebesgue. Αφού κάθε φραγμένο υποσύνολο ![]() του
του ![]() περιέχεται σε κάποιο διάστημα
περιέχεται σε κάποιο διάστημα
![]() και από την στιγμή που το εξωτερικό μέτρο Lebesgue είναι εξωτερικό μέτρο,
δηλαδή ισχύει η ιδιότητα (2), έχουμε ότι
και από την στιγμή που το εξωτερικό μέτρο Lebesgue είναι εξωτερικό μέτρο,
δηλαδή ισχύει η ιδιότητα (2), έχουμε ότι
![]() .
.
Απόδειξη: Έχουμε ότι
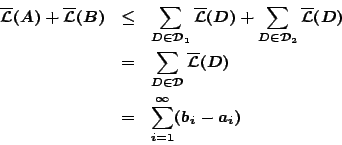
Η προηγούμενη πρόταση 2.2.5 προσδιορίζει προσεγγιστικά από έξω
το εξωτέρικο μέτρο
![]() ενός συνόλου
ενός συνόλου
![]() χρησιμοποιόντας ανοιχτά σύνολα. Μπορούμε
ανάλογα να ορίσουμε το εσωτερικό μέτρο Lebesgue που θα προσεγίζει το σύνολο από
μέσα. Σ''αύτην την περίπτωση όμως, χρησιμοποιούμε συμπάγεις σύνολα (και όχι ανοιχτά όπως προηγουμένος).
χρησιμοποιόντας ανοιχτά σύνολα. Μπορούμε
ανάλογα να ορίσουμε το εσωτερικό μέτρο Lebesgue που θα προσεγίζει το σύνολο από
μέσα. Σ''αύτην την περίπτωση όμως, χρησιμοποιούμε συμπάγεις σύνολα (και όχι ανοιχτά όπως προηγουμένος).
Με άλλα λόγια, το εσωτερικό μέτρο Lebesgue του σύνολου ![]() ισούται με το εξωτερικό μέτρο Lebesgue του
((μεγαλύτερου)) συμπαγούς σύνολου
ισούται με το εξωτερικό μέτρο Lebesgue του
((μεγαλύτερου)) συμπαγούς σύνολου ![]() που χωράει στο
που χωράει στο ![]() . Λέγοντας ((μεγαλύτερο)) εννοούμε ότι όλα τα υπόλοιπα συμπαγείς
υποσύνολα του
. Λέγοντας ((μεγαλύτερο)) εννοούμε ότι όλα τα υπόλοιπα συμπαγείς
υποσύνολα του ![]() είναι υποσύνολα του
είναι υποσύνολα του ![]() .
.
Απόδειξη: Έχουμε ότι το
Θα χρειαστούμε ξανά κάποιο λόγο που να μας ενδιαφέρει η κατασκευή που φτιάξαμε
Έστω τώρα ![]() . Αν
. Αν ![]() είναι συμπαγής, τότε το
είναι συμπαγής, τότε το ![]() καλύπτεται από το διάστημα
καλύπτεται από το διάστημα ![]() , δηλαδή
, δηλαδή
![]() . Άρα
. Άρα
![]() . Από την άλλη, αν
. Από την άλλη, αν
![]() τότε το σύνολο
τότε το σύνολο
![]() είναι συμπαγής, και
είναι συμπαγής, και
![]() . Αυτό ισχύει για όλα τα θετικά
. Αυτό ισχύει για όλα τα θετικά ![]() ,
άρα
,
άρα
![]() . Δηλαδή
. Δηλαδή
![]() .
.
Έχουμε δείξει στο λήμμα 2.2.2
ότι το εσωτερίκο μέτρο Lebesgue είναι μονότονη συνάρτηση άρα για το διάστηματα ![]() ισχυει
ισχυει
![]() .
.
Ομοίως ισχύει ότι
![]() .
.
![]()
Απόδειξη: Αν
Εν γένει η ισότητα
![]() δεν ισχύει, αλλα οταν ισχύει λέμε ότι το σύνολο
δεν ισχύει, αλλα οταν ισχύει λέμε ότι το σύνολο ![]() είναι Lebesgue μετρήσιμο. Πιο αυρτηρός
μαθηματικός ορισμός είναι
είναι Lebesgue μετρήσιμο. Πιο αυρτηρός
μαθηματικός ορισμός είναι
Στην περίπτωση που
![]() τότε το
τότε το ![]() είναι
Lebesgue μετρήσιμο αν και μόνο αν
είναι
Lebesgue μετρήσιμο αν και μόνο αν ![]() είναι
Lebesgue μετρήσιμο για όλα τα
είναι
Lebesgue μετρήσιμο για όλα τα
![]() και το
μέτρο Lebesgue ισούται με το
άπειρο. Γράφουμε
και το
μέτρο Lebesgue ισούται με το
άπειρο. Γράφουμε
![]() για την κοινή τιμή του μέτρου Lebesgue.
για την κοινή τιμή του μέτρου Lebesgue.
Μάζι με την πρόταση 2.2.7 δείξαμε ότι
![]() είναι Lebesgue μετρήσιμο και
είναι Lebesgue μετρήσιμο και
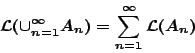
Έστω τώρα ![]() είναι κλειστό υποσύνολο του
είναι κλειστό υποσύνολο του ![]() , τότε για κάθε
, τότε για κάθε
![]() , η τομή
, η τομή ![]() είναι συμπαγή
από θεώρημα 1.5.5 ως κλειστό και φραγμένο υποσύνολο του
είναι συμπαγή
από θεώρημα 1.5.5 ως κλειστό και φραγμένο υποσύνολο του ![]() . Άρα το
. Άρα το ![]() είναι Lebesgue
μετρήσιμο
είναι Lebesgue
μετρήσιμο
Τέλος έστω ![]() είναι ανοιχτό υποσύνολο του
είναι ανοιχτό υποσύνολο του ![]() . Κάθε ανοιχτό υποσύνολο του
. Κάθε ανοιχτό υποσύνολο του ![]() μπόρει να γραφτεί
ως ένωση ανοιχτών διαστημάτων,
μπόρει να γραφτεί
ως ένωση ανοιχτών διαστημάτων,
![]() . Τώρα κάθε σύνολο
. Τώρα κάθε σύνολο
![]() είναι μια ένωση από πεπερασμένα διαστήματα έτσι ώστε το σύνολο
είναι μια ένωση από πεπερασμένα διαστήματα έτσι ώστε το σύνολο ![]() να είναι αριθμήσιμη ένωση ξένων μεταξύ τους
Lebesgue μετρήσιμων συνόλων, άρα το σύνολο
να είναι αριθμήσιμη ένωση ξένων μεταξύ τους
Lebesgue μετρήσιμων συνόλων, άρα το σύνολο ![]() είναι Lebesgue μετρήσιμο.
είναι Lebesgue μετρήσιμο.
![]()
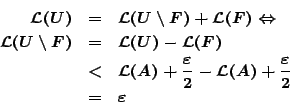
Αντίστροφα, έστω τα σύνολα ![]() και
και ![]() υπάρχουν. υποθέτουμε πρώτα ότι
υπάρχουν. υποθέτουμε πρώτα ότι
![]() .
Τότε
.
Τότε
![]() , αφού
, αφού ![]() . Επιδή
. Επιδή
![]() ,
έχουμε
,
έχουμε
![]() και από την πρόταση
2.2.7 έχουμε ότι
και από την πρόταση
2.2.7 έχουμε ότι
![]() άρα
άρα ![]() είναι Lebesgue μετρήσιμο σύνολο.
είναι Lebesgue μετρήσιμο σύνολο.
Αν
![]() , θέλουμε να δείξουμε ότι τα σύνολα
, θέλουμε να δείξουμε ότι τα σύνολα ![]() είναι Lebesgue μετρήσιμα για
όλα τα
είναι Lebesgue μετρήσιμα για
όλα τα
![]() , κατι το οποίο όμως ισχύει αφού
, κατι το οποίο όμως ισχύει αφού ![]() είναι φραγμενα άρα και το εξωτερικό μέτρο
Lebesgue τους είναι περπερασμένο. Εφαρμόζοντας την πιο πάνω περιπτωση, τελειώσαμε.
είναι φραγμενα άρα και το εξωτερικό μέτρο
Lebesgue τους είναι περπερασμένο. Εφαρμόζοντας την πιο πάνω περιπτωση, τελειώσαμε.
![]()
Απόδειξη: Για να είναι
Μη αρνητική είναι αφού
![]() για το ίδιο λόγο
για το ίδιο λόγο
![]() .
Όσο αφορά την σ-προσθετικότητα, ισχύει από το θεώρημα 2.2.1
.
Όσο αφορά την σ-προσθετικότητα, ισχύει από το θεώρημα 2.2.1
Τώρα για να δείξουμε ότι η ![]() ορίζεται σε μια σ-άλγεβρα θα πρέπει να δείξουμε ότι τα Lebesgue μετρήσιμα σύνολα
αποτελούν την σ-άλγεβρα στο
ορίζεται σε μια σ-άλγεβρα θα πρέπει να δείξουμε ότι τα Lebesgue μετρήσιμα σύνολα
αποτελούν την σ-άλγεβρα στο ![]() . Θα δείξω πρώτα ότι είναι άλγεβρα.
Από προτάση 2.2.8 έχουμε ότι το κενό σύνολο είναι
Lebesgue μετρήσιμο γιατί είναι συμπαγής. Το
. Θα δείξω πρώτα ότι είναι άλγεβρα.
Από προτάση 2.2.8 έχουμε ότι το κενό σύνολο είναι
Lebesgue μετρήσιμο γιατί είναι συμπαγής. Το ![]() είναι Lebesgue μετρήσιμο γιατί είναι κλείστο.
Αν
είναι Lebesgue μετρήσιμο γιατί είναι κλείστο.
Αν
![]() είναι Lebesgue μετρήσιμο τότε πρέπει
να δείξουμε ότι και τό συμπλήρωμα του είναι Lebesgue μετρήσιμο. Από το προηγούμενο θεώρημα
2.2.2 υπάρχουν σύνολα
είναι Lebesgue μετρήσιμο τότε πρέπει
να δείξουμε ότι και τό συμπλήρωμα του είναι Lebesgue μετρήσιμο. Από το προηγούμενο θεώρημα
2.2.2 υπάρχουν σύνολα ![]() και
και ![]() ανοιχτό και κλειστό αντίστοιχα, τέτοια
ώστε
ανοιχτό και κλειστό αντίστοιχα, τέτοια
ώστε
![]() και
και
![]() . Έχουμε ότι τα σύνολα
. Έχουμε ότι τα σύνολα
![]() και
και
![]() είναι ανοιχτό και κλειστό αντίστοιχα (αφού είναι
συμπληρώματα του κλειστού και ανοιχτού συνόλου αντίστοιχα) και ισχύει ότι
είναι ανοιχτό και κλειστό αντίστοιχα (αφού είναι
συμπληρώματα του κλειστού και ανοιχτού συνόλου αντίστοιχα) και ισχύει ότι
![]() . Τώρα πάλι βάσει του θεωρήματος
2.2.2 και του γεγονοτος ότι
. Τώρα πάλι βάσει του θεωρήματος
2.2.2 και του γεγονοτος ότι
![]() , το συμπλήρωμα του
, το συμπλήρωμα του ![]() είναι Lebesgue μετρήσιμο σύνολο. Έμεινε να δείξουμε ότι αν
είναι Lebesgue μετρήσιμο σύνολο. Έμεινε να δείξουμε ότι αν
![]() είναι Lebesgue μετρήσιμα σύνολα, τότε η τομή τους είναι και αυτή Lebesgue
μετρήσιμη. Έχουμε αν
είναι Lebesgue μετρήσιμα σύνολα, τότε η τομή τους είναι και αυτή Lebesgue
μετρήσιμη. Έχουμε αν
![]() και
και
![]() (με
(με ![]() κλειστα συνολα,
κλειστα συνολα, ![]() ανοιχτά σύνολα και
ανοιχτά σύνολα και
![]() ) τότε
) τότε
![]() και
και
![]() . Από αυτά συνεπάγεται πως
. Από αυτά συνεπάγεται πως ![]() είναι μετρήσιμο. Επαγωγικά ισχύει για πεπερασμένες τόμες. Δειξαμε λοιπον οτι τα Lebesgue μετρήσιμα σύνολα
αποτελουν άλγεβρα. Έχουμε δείξει επιπλέον ότι η
είναι μετρήσιμο. Επαγωγικά ισχύει για πεπερασμένες τόμες. Δειξαμε λοιπον οτι τα Lebesgue μετρήσιμα σύνολα
αποτελουν άλγεβρα. Έχουμε δείξει επιπλέον ότι η ![]() είναι σ-προσθετική, οπότε από την πρόταση
2.1.1 τα Lebesgue μετρήσιμα σύνολα είναι σ-άλγεβρα. Αυτό ολοκλειρώνει την απόδειζη.
είναι σ-προσθετική, οπότε από την πρόταση
2.1.1 τα Lebesgue μετρήσιμα σύνολα είναι σ-άλγεβρα. Αυτό ολοκλειρώνει την απόδειζη.
![]()
Τώρα θα δείξουμε πότε ένα εξωτερικό μέτρο γίνεται μέτρο (με την έννοια του Καραθεοδωρη).