




Next: Μέτρο
Up: Θεωρία Μέτρου
Previous: Θεωρία Μέτρου
Contents
Index
Οι σ-άλγεβρες αποτελούν το πεδίο ορισμού για την συνολοσυνάρτηση που θα ορίσουμε να καλείται
μέτρο. Στην παράγραφο αύτη θα ασχοληθούμε με την σ-άλγεβρα, ορίζοντας και μελετώντας
διάφορες ιδιότητές της.
Ορισμός 2.1.1
Μια οικογένεια 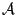 υποσυνόλων ενός συνόλου
υποσυνόλων ενός συνόλου  λέγεται
σ-άλγεβρα στο
λέγεται
σ-άλγεβρα στο  αν ικανοποιεί τις παρακάτω ιδιότητες
αν ικανοποιεί τις παρακάτω ιδιότητες
-
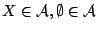
- Αν
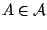 τότε
τότε
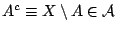
- Αν
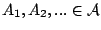 τότε
τότε
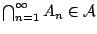
Με την ιδιότητα (1) απαιτούμε το κενό σύνολο να ανήκει στην
σ-άλγεβρα και με τις ιδιότητες (2) και (3) απαιτούμε η σ-άλγεβρα
να είναι κλειστή ως προς τα συμπληρώματα και τις αριθμήσιμες τομές
αντίστοιχα. Ισοδύναμα, στην θέση της ιδιότητας (3) θα μπορούσαμε
να ζητήσουμε να ικανοποιείται
- 3'
- Αν
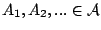 τότε
τότε
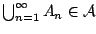
δηλαδή η σ-άλγεβρα να είναι κλειστή ως προς αριθμήσιμες ενώσεις.
Απόδειξη: Στην περίπτωση που ισχύει η (3) έχουμε
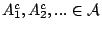 από την (2), τότε όμως από την
(3) έχουμε
από την (2), τότε όμως από την
(3) έχουμε
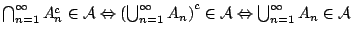 .
.

Θα ορίσουμε τώρα την άλγεβρα. Ο λόγος που το κάνουμε είναι ότι σε μερικές περιπτώσεις η άλγεβρα θα αποτελεί το ενδιάμεσο
στάδιο πριν την σ-άλγεβρα.
Ορισμός 2.1.2
Μια οικογένεια 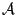 υποσυνόλων ενός συνόλου
υποσυνόλων ενός συνόλου  λέγεται
άλγεβρα στο
λέγεται
άλγεβρα στο  αν ικανοποιεί τις παρακάτω ιδιότητες
αν ικανοποιεί τις παρακάτω ιδιότητες
-
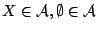
- Αν
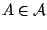 τότε
τότε
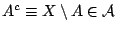
- Αν
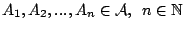 τότε
τότε
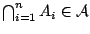
Όπως είναι φανερό η μόνη διαφόρα της άλγεβρας από τη σ-άλγεβρα
βρίσκεται στην ιδιότητα (3) η οποία απαιτεί η άλγεβρα να είναι κλειστή
ως προς πεπερασμένες τομές (όχι αριθμήσιμες όπως στην
σ-άλγεβρα). Επιπλέον όπως και στην σ-άλγεβρα η τρίτη ιδιότητα
είναι ισοδύναμη με αριθμήσιμες ενώσεις έτσι και στην άλγεβρα
μπορούμε να απαιτήσουμε, αντί της τρίτης ιδιότητας, η άλγεβρα να είναι
κλειστή ως προς τις πεπερασμένες ενώσεις.
Είναι προφανές ότι κάθε σ-άλγεβρα είναι και άλγεβρα. Το
αντίθετο δεν ισχύει πάντοτε. Στην επόμενη πρόταση θα δείξουμε
μια περίπτωση όταν μια άλγεβρα είναι σ-άλγεβρα.
Πρόταση 2.1.1
Έστω 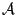 άλγεβρα στο
άλγεβρα στο  . Αν για κάθε ακολουθία
. Αν για κάθε ακολουθία 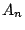 ξένων ανά δύο στοιχείων της
ξένων ανά δύο στοιχείων της 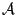 ισχύει
ισχύει
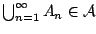 τότε η
τότε η 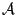 είναι σ-άλγεβρα.
είναι σ-άλγεβρα.
Απόδειξη: Αφού η 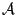 είναι άλγεβρα, αρκεί να δείξουμε ότι η
είναι άλγεβρα, αρκεί να δείξουμε ότι η 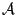 είναι κλειστή ως προς αριθμήσιμες τομές ή ενώσεις (θα το κάνουμε
για ενώσεις). Έστω
είναι κλειστή ως προς αριθμήσιμες τομές ή ενώσεις (θα το κάνουμε
για ενώσεις). Έστω 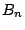 ακολουθία στην
ακολουθία στην 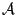 .
.
Θέτουμε
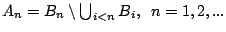 . Τότε
. Τότε
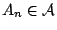 , τα
, τα 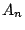 είναι ξένα ανα δύο μεταξύ τους και
είναι ξένα ανα δύο μεταξύ τους και
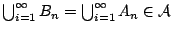 .
.

Θα δώσουμε μερικά παραδείγματα σ-άλγεβρων.
Παράδειγμα: Για οποιοδήποτε σύνολο  η οικογένεια
η οικογένεια
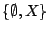 και το δυναμοσύνολο
και το δυναμοσύνολο
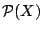 είναι σ-άλγεβρες στο
είναι σ-άλγεβρες στο  . Μάλιστα η πρώτη είναι η ελάχιστη και η δεύτερη η μέγιστη σ-άλγεβρα στο
. Μάλιστα η πρώτη είναι η ελάχιστη και η δεύτερη η μέγιστη σ-άλγεβρα στο 
Παράδειγμα: Έστω
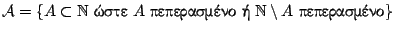 τότε η
τότε η 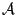 είναι άλγεβρα αλλά όχι σ-άλγεβρα στο
είναι άλγεβρα αλλά όχι σ-άλγεβρα στο 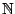
Παράδειγμα: Έστω 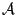 οικογένεια υποσυνόλων του
οικογένεια υποσυνόλων του  για την οποία ισχύει
για την οποία ισχύει
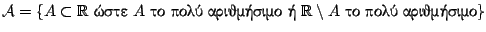 τότε
τότε 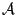 είναι σ-άλγεβρα στο
είναι σ-άλγεβρα στο 
Θα διατυπώσουμε ένα θεώρημα το οποίο μας εξασφαλίζει, πως ο
ορισμός που θα δώσουμε στην συνέχεια για τα σύνολα Borel,
έχει νόημα.
Θεώρημα 2.1.1
Αν 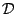 είναι μια οικογένεια υποσυνόλων ενός συνόλου
είναι μια οικογένεια υποσυνόλων ενός συνόλου  ,
τότε υπάρχει η ελάχιστη σ-άλγεβρα
,
τότε υπάρχει η ελάχιστη σ-άλγεβρα 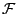 στο
στο  τέτοια
ώστε
τέτοια
ώστε
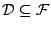 .
.
Απόδειξη: Θα δείξω πως η τομή σ-αλγεβρών στο  είναι και αυτή σ-άλγεβρα
στο
είναι και αυτή σ-άλγεβρα
στο  . Έστω
. Έστω 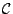 μια συλλογή σ-αλγεβρών στο
μια συλλογή σ-αλγεβρών στο  και
και
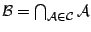 είναι η τομή των στοιχείων της. Έχουμε πως
είναι η τομή των στοιχείων της. Έχουμε πως
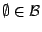 όπως επίσης και
όπως επίσης και
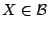 , αφού
και τα δύο σύνολα ανήκουν σε όλες τις σ-άλγεβρες (οπότε θα ανήκουν
και στην τομή). Αν
, αφού
και τα δύο σύνολα ανήκουν σε όλες τις σ-άλγεβρες (οπότε θα ανήκουν
και στην τομή). Αν
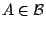 τότε
τότε  θα πρέπει να ανήκει
σ'' όλες τις σ-άλγεβρες
θα πρέπει να ανήκει
σ'' όλες τις σ-άλγεβρες
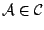 , οπότε και
, οπότε και
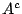 ανήκει σ'' όλες τις σ-άλγεβρες
ανήκει σ'' όλες τις σ-άλγεβρες
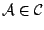 ,
άρα η
,
άρα η
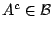 . Τέλος αν
. Τέλος αν
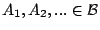 τότε
τότε
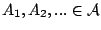 για όλες τις
για όλες τις
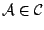 , και άρα
, και άρα
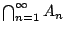 ανήκει σ'' όλες τις
ανήκει σ'' όλες τις
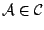 , άρα
, άρα
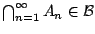
Έστω σύνολο 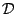 υποσυνόλων του
υποσυνόλων του  ,
και έστω
,
και έστω 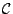 η συλλογή σ-αλγεβρών του
η συλλογή σ-αλγεβρών του  , τέτοιο
ώστε
, τέτοιο
ώστε
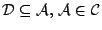 (υπάρχει τουλάχιστον μια τέτοια
σ-άλγεβρα -- το δυναμοσύνολο του
(υπάρχει τουλάχιστον μια τέτοια
σ-άλγεβρα -- το δυναμοσύνολο του  ). Τότε όμως η τομή
). Τότε όμως η τομή
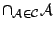 είναι η
σ-άλγεβρα
είναι η
σ-άλγεβρα 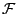 στο
στο  που θέλουμε.
που θέλουμε.
Θα λέμε πως 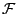 είναι η σ-άλγεβρα στο
είναι η σ-άλγεβρα στο  που παράγεται
από το
που παράγεται
από το 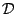

Και τώρα θα ορίσουμε τα σύνολα Borel
Ορισμός 2.1.3
Έστω  μετρικός χώρος. Ένα υποσύνολο του
μετρικός χώρος. Ένα υποσύνολο του  θα λέγεται
σύνολο Borel αν και μόνο ανήκει σε μια σ-άλγεβρα του
θα λέγεται
σύνολο Borel αν και μόνο ανήκει σε μια σ-άλγεβρα του  που παράγεται από ανοικτά σύνολα.
που παράγεται από ανοικτά σύνολα.
Παράδειγμα: Στο 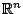 κάθε ανοιχτό ή κλειστό σύνολο είναι σύνολο Borel
κάθε ανοιχτό ή κλειστό σύνολο είναι σύνολο Borel
Πρόταση 2.1.2
Η ένωση ή η τομή κάθε πεπερασμένης η αριθμήσιμης συλλογής συνόλων Borel είναι σύνολο Borel
Λογική συνέπεια είναι ότι οποιοδήποτε σύνολο του  που μπορεί να κατασκευαστεί χρησιμοποιώντας μια ακολουθία
αριθμήσιμων ενώσεων ή τομών ανοιχτών ή κλειστών συνόλων σίγουρα θα είναι σύνολο Borel
που μπορεί να κατασκευαστεί χρησιμοποιώντας μια ακολουθία
αριθμήσιμων ενώσεων ή τομών ανοιχτών ή κλειστών συνόλων σίγουρα θα είναι σύνολο Borel





Next: Μέτρο
Up: Θεωρία Μέτρου
Previous: Θεωρία Μέτρου
Contents
Index
Khusainov Alexander
2002-10-25
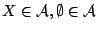
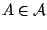 τότε
τότε
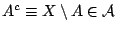
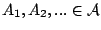 τότε
τότε
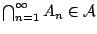
![]() από την (2), τότε όμως από την
(3) έχουμε
από την (2), τότε όμως από την
(3) έχουμε
![]() .
.
![]()
![]() . Τότε
. Τότε
![]() , τα
, τα ![]() είναι ξένα ανα δύο μεταξύ τους και
είναι ξένα ανα δύο μεταξύ τους και
![]() .
.
![]()
![]() η οικογένεια
η οικογένεια
![]() και το δυναμοσύνολο
και το δυναμοσύνολο
![]() είναι σ-άλγεβρες στο
είναι σ-άλγεβρες στο ![]() . Μάλιστα η πρώτη είναι η ελάχιστη και η δεύτερη η μέγιστη σ-άλγεβρα στο
. Μάλιστα η πρώτη είναι η ελάχιστη και η δεύτερη η μέγιστη σ-άλγεβρα στο ![]()
![]() τότε η
τότε η ![]() είναι άλγεβρα αλλά όχι σ-άλγεβρα στο
είναι άλγεβρα αλλά όχι σ-άλγεβρα στο ![]()
![]() οικογένεια υποσυνόλων του
οικογένεια υποσυνόλων του ![]() για την οποία ισχύει
για την οποία ισχύει
![]() τότε
τότε ![]() είναι σ-άλγεβρα στο
είναι σ-άλγεβρα στο ![]()
![]() υποσυνόλων του
υποσυνόλων του ![]() ,
και έστω
,
και έστω ![]() η συλλογή σ-αλγεβρών του
η συλλογή σ-αλγεβρών του ![]() , τέτοιο
ώστε
, τέτοιο
ώστε
![]() (υπάρχει τουλάχιστον μια τέτοια
σ-άλγεβρα -- το δυναμοσύνολο του
(υπάρχει τουλάχιστον μια τέτοια
σ-άλγεβρα -- το δυναμοσύνολο του ![]() ). Τότε όμως η τομή
). Τότε όμως η τομή
![]() είναι η
σ-άλγεβρα
είναι η
σ-άλγεβρα ![]() στο
στο ![]() που θέλουμε.
που θέλουμε.
![]() είναι η σ-άλγεβρα στο
είναι η σ-άλγεβρα στο ![]() που παράγεται
από το
που παράγεται
από το ![]()
![]()
![]() κάθε ανοιχτό ή κλειστό σύνολο είναι σύνολο Borel
κάθε ανοιχτό ή κλειστό σύνολο είναι σύνολο Borel
![]() που μπορεί να κατασκευαστεί χρησιμοποιώντας μια ακολουθία
αριθμήσιμων ενώσεων ή τομών ανοιχτών ή κλειστών συνόλων σίγουρα θα είναι σύνολο Borel
που μπορεί να κατασκευαστεί χρησιμοποιώντας μια ακολουθία
αριθμήσιμων ενώσεων ή τομών ανοιχτών ή κλειστών συνόλων σίγουρα θα είναι σύνολο Borel