Μέθοδος Καραθεοδωρή

Έστω $X$ μετρικός χώρος, $\mathcal{A}$ μια κάλυψη του $X$ και $C:\mathcal{A}\rightarrow[0,\infty]$ μια συνολοσυνάρτηση. Για $\varepsilon>0$ και $B\in X$ ορίζουμε

$$\mathcal{\overline{M}_\varepsilon}(B)=\inf\left\{\sum_{i=1}... ...font diam}A_i\leq\varepsilon,\, A_i\in\mathcal{A} \right\}$$

Για να μην έχουμε πρόβλημα ύπαρξης των $A_i$, υποθέτουμε ότι για κάθε $\varepsilon>0$ υπάρχουν $A_1, A_2,\ldots\in \mathcal{A}$ τέτοια ώστε $\mathop{\operator@font diam}A_i\leq\varepsilon$ και $B=\bigcup^{\infty}_{i=1} A_i$.

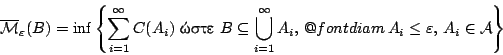
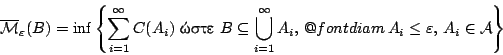
Στην ουσία κατασκευάζουμε ένα εξωτερικό μέτρο που είναι όσο πιο κοντά γίνεται στην δοθείσα συνάρτηση $C$ (μπορεί και ίσο με τη $C$, αν η $C$ είναι η ίδια εξωτερικό μέτρο).

Για να έχει νόημα η κατασκευή, θα πρέπει να δείξουμε πως $\overline{\mathcal{M}}_\varepsilon$ είναι πρώτον μοναδικό (για δοθέν συνάρτηση $C$) και δεύτερον ότι είναι όντως εξωτερικό μέτρο. Η μοναδικότητα εξασφαλίζεται ως λογική συνέπεια της μοναδικότητας του κάτω πέρας(infimum).

Πρώτον $\overline{\mathcal{M}}_\varepsilon (\emptyset)=0$, αφού το κενό σύνολο καλύπτεται από κενή κάλυψη, και επειδή το άθροισμα μη αρνητικών αριθμών δεν μπορεί να είναι αρνητικός αριθμός, συμπεραίνουμε πως το ελάχιστο είναι 0. Αν $A\subseteq B\subseteq X$ τότε οποιαδήποτε κάλυψη του $Β$ είναι και κάλυψη του $Α$ οπότε $\overline{\mathcal{M}}_\varepsilon (Β)\geq \overline{\mathcal{M}}_\varepsilon (A)$. Μένει να δείξουμε την αριθμήσιμη υποπροσθετικότητα. Έστω $A_1, A_2,\ldots\in X$ τότε πρέπει ν.δ.ο

$$\mathcal{\overline{M}_\varepsilon}\left(\bigcup_{n\in\mathb... ...q \sum_{n=1}^{\infty}\mathcal{\overline{M}_\varepsilon}(A_n)$$

Στην περίπτωση που για κάποιο $n$ έχουμε ότι $\mathcal{\overline{M}_\varepsilon}(A_n)=\infty$ τότε τελειώσαμε. Για αυτό μπορούμε να υποθέσουμε ότι για όλα τα $n$ τα $\mathcal{\overline{M}_\varepsilon}(A_n)<\infty$. Έστω $\delta>0$ τότε διαλέγω τέτοιες καλύψεις από την $\mathcal{A}$ ώστε:

$$\overline{\mathcal{M}}_\varepsilon(Α_1) + \delta\left(\fra... ...tor@font diam}E_{1,i}\leq\varepsilon,\, E_{1,i}\in\mathcal{A}$$

$$\overline{\mathcal{M}}_\varepsilon(Α_2) + \delta\left(\fra... ...tor@font diam}E_{2,i}\leq\varepsilon,\, E_{2,i}\in\mathcal{A}$$

$\vdots$

$$\overline{\mathcal{M}}_\varepsilon(Α_n) + \delta\left(\fra... ...tor@font diam}E_{n,i}\leq\varepsilon,\, E_{n,i}\in\mathcal{A}$$

Τώρα $\bigcup_{n=1}^{\infty}A_n\subseteq\bigcup_{n=1}^{\infty}\bigcup_{n=1}^{\infty}E_{n,i}$ όποτε από την κατασκευή έχουμε πως

$$\begin{eqnarray*} \overline{\mathcal{M}}_\varepsilon\left(\bigcup_{n=1}^{\infty... ...{n=1}^{\infty}\overline{\mathcal{M}}_\varepsilon(Α_n) + \delta \end{eqnarray*}$$

Από την στιγμή που $\delta$ είναι οποιοσδήποτε θετικός (μπορεί δηλαδή και πολυ κοντά στο μηδέν) η αρχική ανισότητα ισχύει.

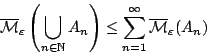
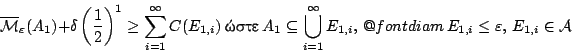
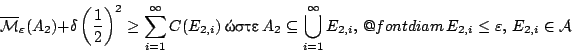
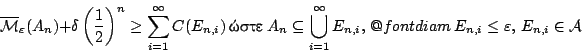
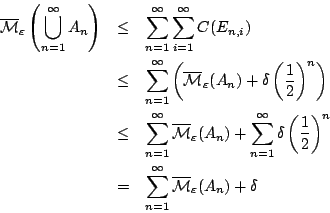
Το εξωτερικό μέτρο $\overline{\mathcal{M}}_\varepsilon$ λέγεται και εξωτερικό μέτρο της Μεθόδου Ι.

Αν πάρουμε $0<\varepsilon<\delta<\infty$ έχουμε ότι $\overline{\mathcal{M}}_\varepsilon>\overline{\mathcal{M}}_\delta$, οπότε έχει νόημα να ορίσουμε το όριο (δεν είναι μηδέν). Για $A\in X$, ορίζουμε

$$\overline{\mathcal{M}}(A)=\lim_{\varepsilon\rightarrow 0}\overline{\mathcal{M}}_\varepsilon(A)$$

Το εξωτερικό μέτρο $\overline{\mathcal{M}}$ λέγεται και εξωτερικό μέτρο της Μεθόδου ΙΙ.