Περιγραφή του Αλγορίθμου

Για την περιγράφη του αλγορίθμου της ((fractal συμπίεση)) θα εισάγουμε κάποιους ορισμούς.

Ορισμός 4.2.1   Block είναι τετραγωνικό τμήμα της εικόνας καθορισμένου μεγέθους $n$. Συμβολίζουμε με $b$ το block και με $b_{i,j}$ την ένταση του pixel στην σχετική θέση του block $i,j$, $0\leq i,j<n$.

Ορισμός 4.2.2   Domen είναι τετραγωνικό μερος της εικόνας διπλάσιο του block. Συμβολίζουμε με $d$ το domen , και με $d_{i,j}$ την ένταση του pixel στην σχετική θέση του domain $i,j$, $0\leq i,j<2n$.

Ορισμός 4.2.3   Μέση τετραγωνική απόκλιση, είναι ένας από τους τρόπους να μετράει κανείς την διαφορά της έντασης μεταξύ των bloks ή domens ίδιου μεγέθους.

$$\hbox{Μ.Τ.Α.}(b,c)=\frac{1}{n^2}\sqrt{\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}(b_{i,j}-c_{i,j})^2}$$

όπου οι διαστάσεις των $b$ και $c$ είναι $0\leq i,j<n$.

Ορισμός 4.2.4   Η μέση ένταση του blok , είναι η τετραγωνική ρίζα του αθροίσματος των εντάσεων όλων των pixels προς το τετράγωνο του μεγέφους του blok .

$$G_0(b)=\frac{1}{n^2}\sqrt{\sum_{i=0}^{n-1}b_{i,j}}$$

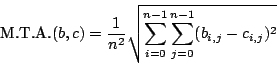
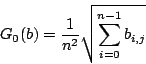
Μέση τετραγωνική απόκλιση από την μέση ένταση είναι μέση τετραγωνική απόκληση του blok (ή του domain) από ένα blok (ή του domain) πού έχει τις διαστάσεις του blok (ή του domain αντίστοιχα) αλλά όλα τα pixels έχουν ένταση $1$.

Επιλπέον για δοσμένο $\varepsilon>0$, που είναι η επιτρεπτη διαφορα μεταξύ πρωτότυπης εικόνας και συμπιεσμένης (με αλλα λόγια εκφράζει την απώλεια, όσο πιο μικρότερο το $\varepsilon$ τόσο λιγότερη είναι η απώλεια), θεώρουμε μονότονο το blok αν η μέση τετραγωνική απόκλιση του απο το block που έχει το ίδιο μέγεθος με όλα τα pixels να έχουν την ένταση ίση με την μέση ένταση του.

Στό πρώτο κεφάλαιο έχουμε ορίσει την συσχετιζόμενη συνάρτηση, ορισμός 1.7.3, και δείξαμε ότι όταν απείκονίζει ένα διάστημα στο $\mathbb{R}$ τότε είναι αναγκαστικά της μορφής $f(x)=\alpha x +\beta$, δηλαδή χρειαζόμαστε μόνο δύο μεταβλήτες για να προσδιορίσουμε μια συσχετιζόμενη συνάρτηση από το $\mathbb{R}$ στο $\mathbb{R}$. Όταν μια συσχετιζόμενη συνάρτηση είναι από το $\mathbb{R}^2$ στο $\mathbb{R}^2$ είναι της μορφής

$$f\left(\matrix{x\cr y}\right)=\left(\matrix{\alpha_{1,1} & ... ...trix{x\cr y}\right) +\left(\matrix{\beta_1\cr \beta_2}\right)$$

δηλαδή μπορούμε να περιγράψουμε πλήρως μια οποιαδήποτε συσχετιζόμενη συνάρτηση από το $\mathbb{R}^2$ στο $\mathbb{R}^2$ με την βοήθεια έξι (μόνο) αριθμών. Ο λόγος που αναφερόμαστε στις συσχετιζόμενες συναρτήσεις είναι ότι αυτές αποτελούν μεγάλο μέρος των συστολών και είναι σχετικά εύκολη η αποτύπωσή τους (καταγραφή). (Αυτό που λέγαμε σχετικά με την διαφορά μεταξύ της πληροφορίας και των δεδομένων, μια συστολή που είναι ταυτόχρονα και συσχετιζόμενη συνάρτηση αποθηκεύται πολύ απλά μόνο με έξι αριθμούς.)

Για να μπορούμε να βρούμε το κατάλληλο σύστημα επαναλαμβανόμενων συναρτήσεων θα περιοριστούμε στην διακριτή επιλογή των συσχετιζόμενων (συστολών) συναρτήσεων. Επιπλέον θα θεωρούμε ότι κάθε σύστημα επαναλαμβανόμενων συναρτήσεων που θα ψάχνουμε, θα αποτελείται από τρεις κλάσεις συσχετιζόμενων συστολών: όπου μία θα αντιπροσωπεύει το γεωμετρικο μέρος, άλλη την περιστροφή και η τρίτη την αλλαγή της φωτεινότητας και του contrast των εικονοστοιχείων.

Αυτό που κάνουν οι συσχετιζόμενες συστολες του γεωμετρικού μέρους είναι να συμπιέζουν το Domain δυο φορες και να το μεταφέρουν στην θέση του block. Δηλαδή είναι της μορφής

$$g\left(\matrix{x\cr y}\right)=\left(\matrix{\frac{1}{2} & 0... ...trix{x\cr y}\right) +\left(\matrix{\beta_1\cr \beta_2}\right)$$

όπου $\beta_1$ και $\beta_2$ είναι οι συντελεστές μεταφοράς (στο επίπεδο).

Η περιστροφή μετασχηματίζει ένα block της εικόνας με έναν από τους παρακάτω τρόπους

1. Ταυτοτικός μετασχηματισμός, δηλαδή αφήνει το block όπως είναι
   
   $$r\left(\matrix{x\cr y}\right)=\left(\matrix{1 & 0\cr 0&1}\r... ...) \left(\matrix{x\cr y}\right) +\left(\matrix{0\cr 0}\right)$$
   
   

2. Συμμετρική ανάκλαση ως προς τον άξονα $x'x$, δηλαδή
   
   $$r\left(\matrix{x\cr y}\right)=\left(\matrix{1 & 0\cr 0&-1}\... ...) \left(\matrix{x\cr y}\right) +\left(\matrix{0\cr 0}\right)$$
   
   

3. Συμμετρική ανάκλαση ως προς τον άξονα $y'y$, δηλαδή
   
   $$r\left(\matrix{x\cr y}\right)=\left(\matrix{-1 & 0\cr 0&1}\... ...) \left(\matrix{x\cr y}\right) +\left(\matrix{0\cr 0}\right)$$
   
   

4. Συμμετρική ανάκλαση ως προς την κύρια διαγώνιο, δηλαδή
   
   $$r\left(\matrix{x\cr y}\right)=\left(\matrix{0 & 1\cr 1&0}\r... ...) \left(\matrix{x\cr y}\right) +\left(\matrix{0\cr 0}\right)$$
   
   

5. Συμμετρική ανάκλαση ως προς την δεύτερη διαγώνιο, δηλαδή
   
   $$r\left(\matrix{x\cr y}\right)=\left(\matrix{0 & -1\cr -1&0}... ...) \left(\matrix{x\cr y}\right) +\left(\matrix{0\cr 0}\right)$$
   
   

6. Στροφή κατα $90^{\circ}$, δηλαδή
   
   $$r\left(\matrix{x\cr y}\right)=\left(\matrix{0 & 1\cr -1&0}\... ...) \left(\matrix{x\cr y}\right) +\left(\matrix{0\cr 0}\right)$$
   
   

7. Στροφή κατα $180^{\circ}$, δηλαδή
   
   $$r\left(\matrix{x\cr y}\right)=\left(\matrix{0 & -1\cr -1&0}... ...) \left(\matrix{x\cr y}\right) +\left(\matrix{0\cr 0}\right)$$
   
   

8. Στροφή κατα $-90^{\circ}$, δηλαδή
   
   $$r\left(\matrix{x\cr y}\right)=\left(\matrix{0 &-1\cr 1&0}\r... ...) \left(\matrix{x\cr y}\right) +\left(\matrix{0\cr 0}\right)$$
   
   

Τέλος η τρίτη συσχετιζόμενη συνάρτηση είναι της μορφής

$$bc(b_{i,j})=\alpha b_{i,j} + \Delta$$

όπου $\alpha$ είναι ο πολλαπλασιαστής του contrast και $\Delta$ διαφορά της φωτεινότητας.

Έτσι λοιπόν η σύνθεση τέτοιων συσχετιζόμενων συστολών είναι $f=g\circ r \circ bc$ η συστολή για την οποία μπορούμε να εφαρμόσουμε το θεώρημα .....

Θα προχωρίσουμε τώρα στο δεύτερο βήμα της κατασκευής του αλγορίθμου, δηλαδή στην περιγραφή της μεθόδου διαμέρισης της εικόνας σε κομμάτια. Οπότε πρέπει να ορίσουμε ένα είδος κανόνα χωρισμού της εικόνας σε τμήματα. Έστω ότι το block είναι $n\times n$ εικονοστοιχεία τότε το domain θα είναι $2n\times 2n$. Έστω ότι οι διαστάσεις της εικόνας $X\times Y$ είναι πολλαπλάσια του $n$ (θα το θεωρούμε αυτό και στην συνέχεια). Έτσι μπορούμε να χωρίσουμε την εικόνα σε $(X/n) \times (Y/n)$ ξένα μεταξύ τους block, θα τα συμβολίζουμε $b_i$. Κάθε domain περιέχει τέσσερα block. Δηλαδή μπορούμε να σπάσουμε την αρχική μας εικόνα σε $(X-1)/n \times (Y-1)/n$ domain τα οποία, σε αντίθεση με τα block, τέμνονται. Θα συμβολίζουμε τα domain με $d_j$.

Τέλος θα πρέπει να ορίσουμε την μέθοδο εύρεσης του κατάλληλου συστήματος επαναλαμβανόμενων συναρτήσεων. Ο αλγόριθμος βασίζεται στην εύρεση για κάθε block, $b_i$ τέτοιας δυάδας $(d_j,f_k)$ ωστέ η μέση τετραγωνική απόκληση του $b_i$ από $f_k[d_j]$, να είναι όσο το δυνατόν μικρή, $\hbox{Μ.Τ.Α.}(b_i,f_k[d_j])<\varepsilon$. Παρατηρούμε ότι αν το block είναι μονότονο τότε μπορούμε να το παρουσιάσουμε σαν ένα block που έχει την ένταση όλων των εικονοστοιχείων του ίση με την μέση ένταση του. Όποτε δεν χρεάζεται να ψάξουμε το σύστημα επαναλαμβανόμενων συναρτήσεων γι'' αυτό. Τέλος στην περιπτώση δεν βρίσκουμε κατάλληλο domain στα επιτραπτά όρια και το block δεν είναι μονότονο, μπόρουμε να διαιρέσουμε το block σε τέσσερα κομμάτια διαστάσεων $n/2\times n/2$ εικονοστοιχείων. Γι'' αυτά τα block που πήραμε μετά από τεμαχισμό εφαρμόζουμε την ίδια διαδικασία όπως και πριν.